Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ABCEID?
Gọi diện tích là S
SABD=SCBD ( vì có cùng chiều cao hạ từ đỉnh B xuống đáy AC )
=> SABD=SCBD=156:2=78 cm2
SBAE=SCAE ( vì có cùng chiều cao hạ từ đỉnh A xuống đáy BC )
=> SBAE=SCAE=156:2=78 cm2
SABI=SEBI ( vì có cùng chiều cao hạ từ đỉnh B xuống đáy AE )
=> SABI=SEBI=78:2=39 xm2
=> SAID=78-39=39 cm2
Vậy diện tích tam giác AID = 39 cm2
Nếu bạn thấy dài quá mình cũng có cách ngắn gọn hơn nhưng không biết đúng hay sai
SABD=SCBD ( vì có cùng chiều cao hạ từ đỉnh B xuống đáy AC )
=> SABD=SCBD=156:2=78 cm2
SBAI=SAID ( vì có cùng chiều cao hạ từ đỉnh A xuống đáy BD )
=> SAID=SBAI=78:2=39 cm2
Vậy diện tích tam giác AID = 39 cm2

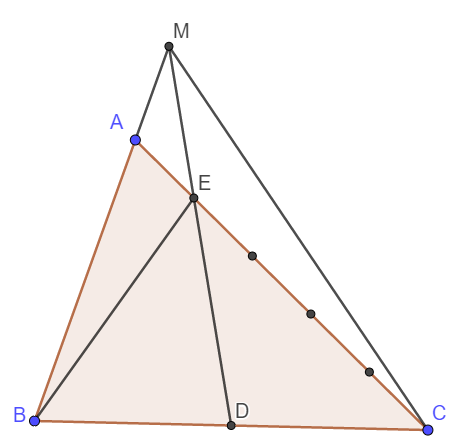
a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên \(S_{MEC}=4S_{MAE}=4\times20=80\left(cm^2\right)\)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên \(S_{MBD}=S_{MCD}\)
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên \(S_{EBD}=S_{ECD}\)
Vậy nên \(S_{MBE}=S_{MEC}=80\left(cm^2\right)\)
Ta có \(\frac{S_{AME}}{S_{MEC}}=\frac{1}{4};\frac{S_{ABE}}{S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{AME}+S_{ABE}}{S_{MEC}+S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{MBE}}{S_{MEBC}}=\frac{1}{4}\)
\(\Rightarrow S_{MEBC}=4.80=320\left(cm^2\right)\)
\(\Rightarrow S_{MBC}=320+80=400\left(cm^2\right)\)
\(\Rightarrow S_{ABC}=400-20-80=300\left(cm^2\right)\)

Cho tam giác ABC. Gọi D là điểm chính giữa của cạnh BC. Lấy E trên cạnh AC sao cho AE bằng 1/5 AC. Nối D với E. Kéo dài DE cắt AB kéo dài tại M. Nối M với C. Biết diện tích AME bằng 20 cm2 .Tính diện tích MEC và ABC?
Được cập nhật 22 tháng 5 2019 lúc 20:10
4
![]()
![]()
Hoàng Thị Thu Huyền Quản lý
7 tháng 3 2018 lúc 10:05

a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên SMEC=4SMAE=4×20=80(cm2)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên SMBD=SMCD
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên SEBD=SECD
Vậy nên SMBE=SMEC=80(cm2)

D là điểm chính giữa của đoạn thẳng BC
=>D là trung điểm của BC
=>BD/BC=1/2
=>\(S_{ABD}=\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{2}\cdot360=180\left(cm^2\right)\)
AE=ED
A,E,D thẳng hàng
Do đó; E là trung điểm của AD
=>\(AE=\dfrac{1}{2}AD\)
=>\(S_{ABE}=\dfrac{1}{2}\cdot S_{ABD}=\dfrac{1}{2}\cdot180=90\left(cm^2\right)\)

Hai tam giác ABE và ABC có chung cao hạ từ A xuống BC đáy BE=1/2 EC hay BE = 1/3 EC
Suy ra SABE = 1/3 SABC
Ta có hình vẽ :
A B C E I D 16 cm2
Nối IC ta có :
+ dt ABI = 2/3 x dt ABE [Vì đáy AI = 2/3 x AE, chung đường cao kẻ từ B tới AE] 1
+ dt ABE = 1/3 x dt ABC [Vì đáy BE = 1/3 x BC, chung đường cao kẻ từ A tới BC] 2
Từ 1 và 2 ta có : dt ABI = 2/3 x 1/3 x dt ABC
= 2/9 x dt ABC
+ dt IEC = 1/3 x dt AEC [Vì đáy IE = 1/3 x AE, chung đường cao kẻ từ C tới AE] 3
+ dt IBE = 1/3 x dt ABE [Vì đáy IE = 1/3 x AE, chung đường cao kẻ từ B tới AE] 4
Từ 3 và 4 ta có : dt IEC + dt IBE = 1/3 x (dt AEC + dt ABE)
dt IBC = 1/3 x dt ABC
Phân số chỉ tỉ số giữa dt tam giác ABI và dt tam giác IBC là :
2/9 : 1/3 = 2/3 x (dt IBC)
- Vì dt ABI = 2/3 x dt IBC mà 2 hình này có chung đáy BD suy ra đường cao kẻ từ A tới BD = 2/3 đường cao kẻ từ C tới BD hay đường cao kẻ từ A tới ID = 2/3 đường cao kẻ từ C tới ID.
+ dt AID = 2/3 x dt CID [Vì chung đáy ID, đường cao kẻ từ A tới ID = 2/3 đường cao kẻ từ C tới ID]
- Vì dt AID = 2/3 x dt CID mà 2 hình này có chung đường cao kẻ từ I tới AC nêm suy ra đáy AD = 2/3 x DC
+ dt AID = 2/3 x dt IDC [Vì đáy AD = 2/3 x DC, chung đường cao kẻ từ I tới AC]
Diện tích tam giác IDC là : 16 : 2/3 = 24 (cm2)
Diện tích tam giác AIC là : 16 + 24 = 40 (cm2)
+ dt AIC = 2/3 x dt AEC [Vì đáy AI = 2/3 x AE, chung đường cao kẻ từ C tới AE]
Diện tích tam giác AEC là : 40 : 2/3 = 60 (cm2)
+ dt AEC = 2/3 dt ABC [Vì đáý EC = 2/3 x BC, chung đường cao kẻ từ A tới BC]
Diện tích tam giác ABC là : 60 : 2/3 = 90 (cm2)