
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


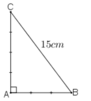
Theo đề bài ta có:
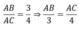
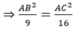
Theo tính chất dãy tỉ số bằng mhau ta có:
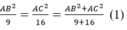
tam giác ABC vuông tại A
Áp dụng định lí pitago vào tam giác ABC ta có:
BC2 = AB2 + AC2 (2)
Từ (1) và (2) suy ra:
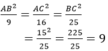
AB2 = 9. 9 = 81 ⇒ AB = 9 cm (vì AB > 0)
AC2 = 16. 9 = 144 ⇒ AC = 12 cm (vì AC > 0)

Mình làm mẫu cho bạn câu a) nhé
a) Theo định lí Pytago ta có :
BC2 = AB2 + AC2
152 = AB2 + AC2
AB : AC = 3:4
=> \(\frac{AB}{3}=\frac{AC}{4}\)=> \(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}\)và AB2 + AC2 = 152
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}=\frac{AB^2+AC^2}{3^2+4^2}=\frac{15^2}{25}=\frac{225}{25}=9\)
\(\frac{AB^2}{3^2}=9\Rightarrow AB^2=81\Rightarrow AB=\sqrt{81}=9cm\)
\(\frac{AC^2}{4^2}=9\Rightarrow AC^2=144\Rightarrow AC=\sqrt{144}=12cm\)
Ý b) tương tự nhé

Ta có: AB = 15cm ; AC = 20cm
=> AB2 + AC2 = 152 + 202 = 225 + 400 = 625 (cm) (1)
BC = 25 => BC2 = 252 = 625 (cm) (2)
Từ (1) và (2) => AB2 + AC2 = BC2
Vậy tam giác ABC vuông tại A (đpcm).
ta có: AB = 15cm ; AC = 20cm
=> AB2 + AC2 = 152 + 202 = 225 + 400 = 625 (cm) (1)
BC = 25 => BC2 = 252 = 625 (cm) (2)
Từ (1) và (2) => AB2 + AC2 = BC2
Vậy tam giác ABC vuông tại A (đpcm).

Bài 1:
A C B
Độ dài cạnh AB: ( 49 + 7 ) : 2 = 28 (cm)
Độ dài cạnh AC: 28 - 7 = 21 (cm)
Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A có:
\(BC^2=AC^2+AB^2\)
Hay \(BC^2=21^2+28^2\)
\(\Rightarrow BC^2=441+784\)
\(\Rightarrow BC^2=1225\)
\(\Rightarrow BC=35\left(cm\right)\)
Bài 2:
A B C D
Áp dụng định lý Py-ta-go vào tam giác ABD vuông tại D có:
\(AB^2=AD^2+BD^2\)
\(\Rightarrow AD^2=AB^2-BD^2\)
Hay \(AD^2=17^2-15^2\)
\(\Rightarrow AD^2=289-225\)
\(\Rightarrow AD^2=64\)
\(\Rightarrow AD=8\left(cm\right)\)
Trong tam giác ABC có:
\(AD+DC=AC\)
\(\Rightarrow DC=AC-AD=17-8=9\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác BCD vuông tại D có:
\(BC^2=BD^2+DC^2\)
Hay \(BC^2=15^2+9^2\)
\(\Rightarrow BC^2=225+81\)
\(\Rightarrow BC^2=306\)
\(\Rightarrow BC=\sqrt{306}\approx17,5\left(cm\right)\)