Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, tam giác ABC vuông tại A (gt) => BC^2 = AC^2 + AB^2 (pytago)
BC = 10; AB = 8 (Gt)
=> AC^2 = 10^2 - 8^2
=> AC^2 = 36
=> AC = 6 do AC > 0
b, xét tam giác AMB và tam giác DMC có : AM = MD (gt)
BM = MC do M là trung điểm của BC(gt)
^BMA = ^DMC (đối đỉnh)
=> tam giác AMB = tam giác DMC (c-g-c)
=> ^ABM = ^MCD mà 2 góc này slt
=> AB // CD
AB _|_ AC
=> CD _|_ AC
c, xét tam giác ACE có : AH _|_ AE
AH = HE
=> tam giác ACE cân tại C
d, xét tam giác BMD và tam giác CMA có L BM = MC
AM = MD
^BMD = ^CMA
=> tam giác BMD = tam giác CMA (c-g-c)
=> BD = AC
AC = CE do tam giác ACE cân tại C (câu c)
=> BD = CE

a) Xét hai tam giác ABM và MCE có:
+ MA = ME
+ góc AMB = góc CME ( 2 góc đối đỉnh )
+ vì M là trung điểm của BC => MB = MC
Vậy tam giác ABM = tam giác MCE ( c - g - c )
b) Vì tam giác ABM = tam giác MCE nên góc ABM = góc MCE ( 2 góc tương ứng)
Mà hai góc này bằng nhau ở vị trí so le trong nên AB // EC (đpcm)

a, tam giác ABC vuông tại A (gt) => BC^2 = AC^2 + AB^2 (pytago)
BC = 10; AB = 8 (Gt)
=> AC^2 = 10^2 - 8^2
=> AC^2 = 36
=> AC = 6 do AC > 0
b, xét tam giác AMB và tam giác DMC có : AM = MD (gt)
BM = MC do M là trung điểm của BC(gt)
^BMA = ^DMC (đối đỉnh)
=> tam giác AMB = tam giác DMC (c-g-c)
=> ^ABM = ^MCD mà 2 góc này slt
=> AB // CD
AB _|_ AC
=> CD _|_ AC
c, xét tam giác ACE có : AH _|_ AE
AH = HE
=> tam giác ACE cân tại C
d, xét tam giác BMD và tam giác CMA có L BM = MC
AM = MD
^BMD = ^CMA
=> tam giác BMD = tam giác CMA (c-g-c)
=> BD = AC
AC = CE do tam giác ACE cân tại C (câu c)
=> BD = CE

1, Xét △ABC vuông tại A có: AC2 + AB2 = BC2 (định lý Pytago)
=> AC2 = BC2 - AB2 = 102 - 82 = 36
=> AC = 6 (cm)
2. Xét △AMB và △DMC
Có: AM = MD (gt)
AMB = DMC (2 góc đối đỉnh)
MB = MC (gt)
=> △AMB = △DMC (c.g.c)
=> MAB = MDC (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong
=> AB // DC (dhnb)
Mà AB ⊥ AC
=> CD ⊥ AC (từ vuông góc đến song song)
3. Xét △AHC và △EHC cùng vuông tại H
Có: CH là cạnh chung
AH = EH (gt)
=> △AHC = △EHC (2cgv)
=> AC = EC (2 cạnh tương ứng)
=> △ACE cân tại C
4, Xét △CAM và △BDM
Có: AM = DM (gt)
CMA = BMD (2 góc đối đỉnh)
CM = MB (gt)
=> △CAM = △BDM (c.g.c)
=> AC = BD (2 cạnh tương ứng)
Mà AC = CE (cmt)
=> BD = CE

a) Xét ΔAMB và ΔDMC có
MA=MD(gt)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔDMC(c-g-c)

Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.

a. Xét tam giác BMC và tam giác DMA có
MB=MD(gt) BMC=DMA(đối đỉnh)
MA=MC(vì M là trung điềm AC)
Vậy tam giác BMC = tam giác DMA(c-g-c)
=>MBC=MDA( 2 góc tương ứng)
=> AD // BC
b. Xét tam giác AMB và tam giác CMD có
MA=MC(vì M là trung điềm AC)
AMB=CMD( đối đỉnh)
MB=MD(gt)
Vậy tam giác AMB = tam giác CMD(c-g-c)
=> AB=CD(2 cạnh tương ứng)
mà AB=AC(vì tam giác ABC cân tại A)
=> AC=CD
=> tam giác ACD cân tại C
c. trong tam giác DEB có M là trung điểm của BD( vì MD=MB)
=> EM là đường trung tuyến thứ nhất (1)
mặt khác AC=CE(gt)
MC=1/2 AC (vì M là trung điềm AC)
=> MC= 1/2 CE

Cách 1: Giải theo phương pháp bậc tiểu học (của bạn Ác Quỷ)
Ta có
Mà dt(AMN) = 1/4 dt(ABN) = 1/4 . 1/2 dt(ABC) = 1/8 dt(ABC)
dt(DMN) = dt(ABC) - dt(AMN) - dt(BDM) - dt(CDN) = dt(ABC) - 1/8 dt(ABC) - 3/8 dt(ABC) - 1/4 dt(ABC) = 1/4 dt(ABC)
Vậy , suy ra AE/AD = 1/3
Cách 2: Giải theo phương pháp bậc THCS (của bạn Lê Quang Vinh)
DN là đường trung bình của tam giác ABC => DN // AB và DN = 1/2 AB
DN // AB => Hai tam giác EAM và EDN đồng dạng => EA/ED = AM/DN = 1/2 (vì AM = 1/4 AB, DN = 1/2 AB)
=> AE/AD = 1/3


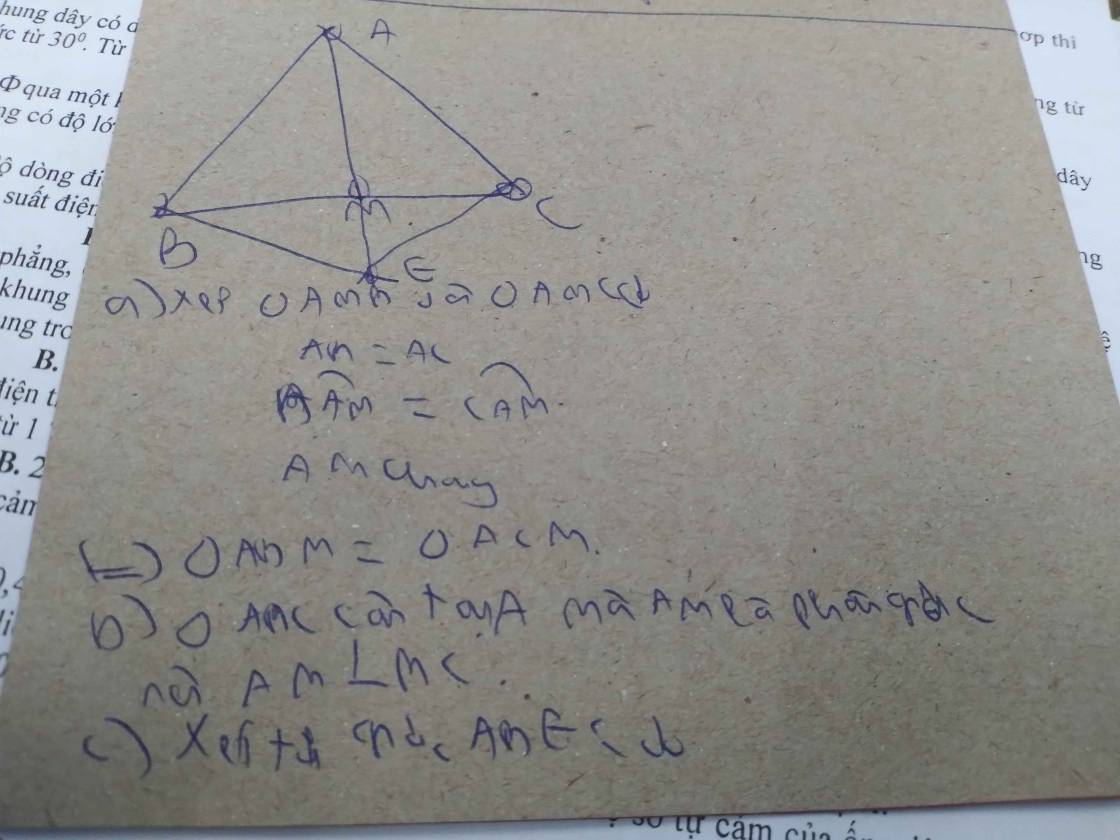

a: Xet ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔAMB=ΔAMC
=>MB=MC
b: Xét ΔMBA và ΔMCE có
MB=MC
\(\widehat{BMA}=\widehat{CME}\)(hai góc đối đỉnh)
MA=ME
Do đó: ΔMBA=ΔMCE
=>\(\widehat{MBA}=\widehat{MCE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE