TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
28 tháng 8 2021
Dựng các đường kính MH,KN như hình : A B D c O N Q M P K N H
Tứ giác ABNK có 4 góc vuông nên :
\(\Rightarrow\)Tứ giác ABNK là hình chữ nhật
Ta có :
\(\hept{\begin{cases}ON=OK\\AM=MB\end{cases}}\)
\(\Rightarrow\)MO là đường trung bình
\(\Rightarrow MO=\frac{BN+AK}{2}=\frac{\frac{1}{2}AB+\frac{1}{2}AD}{2}=\frac{\frac{1}{2}BC}{2}\)
\(=\frac{BC}{2}=\frac{\sqrt{2}}{2}\)
Ta có :
\(OM\perp AB,OH\perp CD,OK\perp AD,ON\perp BC\)
\(\Rightarrow\)MNHK \(\in\left(O\right)\)nội tiếp hình vuông
\(\Rightarrow OM=OH=OK=ON=\frac{\sqrt{2}}{2}\)
PH
2
13 tháng 9 2021
Lời giải:
Gọi dây trên là dây AB. Hạ OH⊥⊥AB = {H} (cd)
Xét (O) 1 phần đường kính OH: OH⊥⊥AB = {H} (cd)
=> H là trung điểm AB (đl) => HA = HB = AB: 2 = 12:2 = 6 (cm)
OH⊥⊥AB = {H} (cd) => ΔΔOHB vuông tại H (đn)
=> OH22+ HB22= OB22(Đl Py-ta-go)
T/s: OH22+ 622= R22
<=> OH22+36 = 1022=100
<=> OH22= 64 => OH = 8 (cm)
13 tháng 9 2021
Gọi H là chân đường cao kẻ từ O
=> H là trung điểm AB
=> AH = AB/2 = 12/2 = 6 cm
Theo định lí Pytago cho tam giác AOH vuông tại H
\(AO^2=OH^2+AH^2\Rightarrow OH^2=AO^2-AH^2=100-36=64\Rightarrow OH=8\)cm
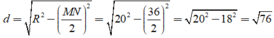
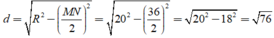
Gọi OK là khoảng cách từ O đến dây MN
Suy ra: K là trung điểm của MN
Xét ΔOMN có OM=ON=MN
nên ΔOMN đều
Xét ΔOKN vuông tại K có
\(ON^2=OK^2+KN^2\)
hay \(OK=\dfrac{R\sqrt{3}}{2}\)