Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
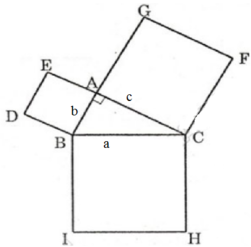
Giả sử tam giác vuông ABC có cạnh huyền là a và hai cạnh góc vuông là b, c.
Diện tích hình vuông dựng trên cạnh huyền a là a2
Diện tích các hình vuông dựng trên hai cạnh góc vuông b, c lần lượt là b2, c2.
Tổng diện tích hai hình vuông dựng trên hai cạnh góc vuông b, c là b2 + c2.
Theo định lí Pitago, tam giác ABC có: a2 = b2 + c2
Vậy: Trong một tam giác vuông, tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích vuông dựng trên cạnh huyền.
Giả sử tam giác vuông ABC có cạnh huyền là a và hai cạnh góc vuông là b, c (hình a).
Diện tích hình vuông dựng trên cạnh huyền a là a2
Diện tích các hình vuông dựng trên hai cạnh góc vuông b, c lần lượt là b2 + c2
Theo định lí Pitago, tam giác vuông ABC có: a2 = b2 + c2
Vậy: Trong một tam giác vuông, tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.
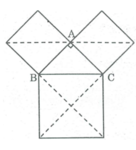
Chú ý: Ta có một cách chứng minh khác đinh lyd Pitago bằng diện tích. Trên hình b, hai hình vuông ABDE và GHIK cùng có cạnh bằng b + c.
Do đó
SABDE = (b+c)2= Sb+ Sc+ 4. (1)
SGHIK= (b+c)2 = Sa + 4. (2)
Từ (1) và (2) suy ra
Sb+ Sc = Sa
tick đúng nha
2 cạnh góc vuông tam giác đó là a;b
=> cạnh huyền là a2+b2
tổng diện tích 2 hình vuông dựng trên 2 cạnh góc vuông là a2+b2
diện tích h.vuông dựng trên cạnh huyền là (a2+b2)2
Tổng diện tích hai hình vuông dựng trên hai cạnh góc vuông b và c là : b² + c²
Diện tích hình vuông dựng trên cạnh huyền là : a².
Theo định lý Pytago có a² = b² + c².
Vậy tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.
Gọi S là diện tích của tam giác ABC.
Hình vuông có cạnh AB được chia thành hai tam giác vuông cân bằng △ ABC nên diện tích hình vuông cạnh AB bằng 2S.
Hình vuông có cạnh AC được chia thành hai tam giác vuông cân bằng △ ABC nên diện tích hình vuông cạnh AC bằng 2S.
Hình vuông cạnh BC được chia thành bốn hình tam giác vuông cân bằng △ ABC nên có diện tích bằng 4S.
Vì 4S = 2S + 2S nên diện tích hình vuông dựng trên cạnh huyền bằng tổng diện tích hai hình vuông dựng trên hai cạnh góc vuông.
Câu hỏi này thực sự ko nghiêm túc, ko cần thiết nên thực sự ko nên trả lời, mong lần sau bn đăng bài quan trọng hơn, ko đăng câu hỏi linh tinh như thế này!
Gọi đọ dài cạnh góc vuông lớn là a.
Ta có:
92=a2+(a-5)2
<=> 81=a2+a2-10a+25
<=> 2a2-10a-56=0
<=> a2-5a-28=0 => \(a=\frac{5+\sqrt{137}}{2}\)
=> Cạnh góc vuông bé là: \(\frac{5+\sqrt{137}}{2}-5=\frac{\sqrt{137}-5}{2}\)
Diện tích miếng đất là: \(S=\frac{1}{2}.\frac{\sqrt{137}+5}{2}.\frac{\sqrt{137}-5}{2}=\frac{1}{8}\left(137-25\right)\)
=> S=112/8 = 14 (m2)
Đáp số: S=14 m2
Giả sử tam giác vuông ABC có cạnh huyền là a và hai cạnh góc vuông là b, c (hình a).
Diện tích hình vuông dựng trên cạnh huyền a là a2
Diện tích các hình vuông dựng trên hai cạnh góc vuông b, c lần lượt là b2 + c2
Theo định lí Pitago, tam giác vuông ABC có: a2 = b2 + c2
Vậy: Trong một tam giác vuông, tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.
Chú ý: Ta có một cách chứng minh khác đinh lyd Pitago bằng diện tích. Trên hình b, hai hình vuông ABDE và GHIK cùng có cạnh bằng b + c.
Do đó
SABDE = (b+c)2= Sb+ Sc+ 4.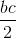
(1)
SGHIK= (b+c)2 = Sa + 4.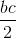
(2)
Từ (1) và (2) suy ra
Sb+ Sc = Sa