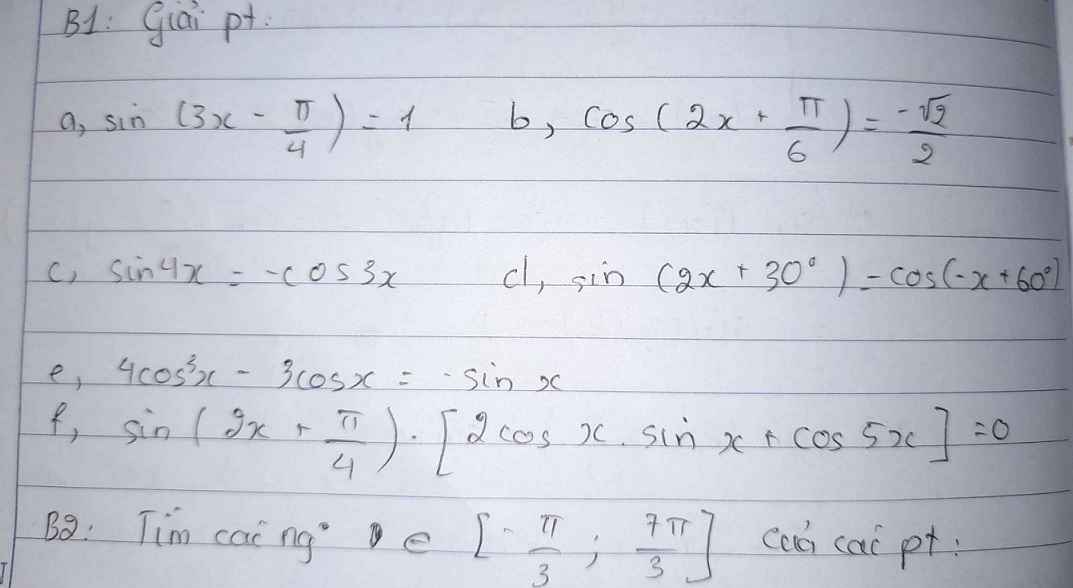K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
1.
\(u_{n+1}=4u_n+3.4^n\)
\(\Leftrightarrow u_{n+1}-\dfrac{3}{4}\left(n+1\right).4^{n+1}=4\left[u_n-\dfrac{3}{4}n.4^n\right]\)
Đặt \(u_n-\dfrac{3}{4}n.4^n=v_n\Rightarrow\left\{{}\begin{matrix}v_1=2-\dfrac{3}{4}.4=-1\\v_{n+1}=4v_n\end{matrix}\right.\)
\(\Rightarrow v_n=-1.4^{n-1}\)
\(\Rightarrow u_n=\dfrac{3}{4}n.4^n-4^{n-1}=\left(3n-1\right)4^{n-1}\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
2.
\(a_n=\dfrac{a_{n-1}}{2n.a_{n-1}+1}\Rightarrow\dfrac{1}{a_n}=2n+\dfrac{1}{a_{n-1}}\)
\(\Leftrightarrow\dfrac{1}{a_n}-n^2-n=\dfrac{1}{a_{n-1}}-\left(n-1\right)^2-\left(n-1\right)\)
Đặt \(\dfrac{1}{a_n}-n^2-n=b_n\Rightarrow\left\{{}\begin{matrix}b_1=2-1-1=0\\b_n=b_{n-1}=...=b_1=0\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{a_n}=n^2+n\Rightarrow a_n=\dfrac{1}{n^2+n}\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
a.
\(sin\left(2x-\dfrac{\pi}{4}\right)=-1\)
\(\Leftrightarrow2x-\dfrac{\pi}{4}=-\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{8}+k\pi\) (1)
\(-\dfrac{\pi}{3}\le x\le\dfrac{7\pi}{3}\Rightarrow-\dfrac{\pi}{3}\le-\dfrac{\pi}{8}+k\pi\le\dfrac{7\pi}{3}\)
\(\Rightarrow-\dfrac{5}{24}\le k\le\dfrac{59}{24}\Rightarrow k=\left\{0;1;2\right\}\)
Thế vào (1) \(\Rightarrow x=\left\{-\dfrac{\pi}{8};\dfrac{7\pi}{8};\dfrac{15\pi}{8}\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
c.
\(\Leftrightarrow sin4x=sin\left(3x-\dfrac{\pi}{2}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=3x-\dfrac{\pi}{2}+k2\pi\\4x=\dfrac{3\pi}{2}-3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{2}+k2\pi\\x=\dfrac{3\pi}{14}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
d.
\(\Leftrightarrow sin\left(2x+30^0\right)=sin\left(30^0+x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+30^0=30^0+x+k360^0\\2x+30^0=150^0-x+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k360^0\\x=40^0+k120^0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
e.
\(\Leftrightarrow cos3x=-sinx\)
\(\Leftrightarrow cos3x=cos\left(\dfrac{\pi}{2}+x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=\dfrac{\pi}{2}+x+k2\pi\\3x=-\dfrac{\pi}{2}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=-\dfrac{\pi}{8}+\dfrac{k\pi}{2}\end{matrix}\right.\)
f.
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)\left(sin2x+cos5x\right)=0\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)\left(sin2x-sin\left(5x-\dfrac{\pi}{2}\right)\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(2x-\dfrac{\pi}{4}\right)=0\\sin\left(5x-\dfrac{\pi}{2}\right)=sin2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{4}=k\pi\\5x-\dfrac{\pi}{2}=2x+k2\pi\\5x-\dfrac{\pi}{2}=\pi-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\\x=\dfrac{3\pi}{14}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2022
1.
\(\lim\left(\sqrt{9^n-2.3^n}-3^n+\dfrac{1}{2021}\right)\)
\(=\lim\left(\dfrac{\left(\sqrt{9^n-2.3^n}-3^n\right)\left(\sqrt{9^n-2.3^n}+3^n\right)}{\sqrt{9^n-2.3^n}+3^n}+\dfrac{1}{2021}\right)\)
\(=\lim\left(\dfrac{-2.3^n}{\sqrt{9^n-2.3^n}+3^n}+\dfrac{1}{2021}\right)\)
\(=\lim\left(\dfrac{-2.3^n}{3^n\left(\sqrt{1-\dfrac{2}{3^n}}+1\right)}+\dfrac{1}{2021}\right)\)
\(=\lim\left(\dfrac{-2}{\sqrt{1-\dfrac{2}{3^n}}+1}+\dfrac{1}{2021}\right)\)
\(=\dfrac{-2}{1+1}+\dfrac{1}{2021}=-\dfrac{2020}{2021}\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2022
2.
\(AP=4PB=4\left(AB-AP\right)=4AB-4AP\)
\(\Rightarrow5AP=4AB\Rightarrow AP=\dfrac{4}{5}AB\)
\(\Rightarrow\overrightarrow{AP}=\dfrac{4}{5}\overrightarrow{AB}\)
\(CD=5CQ=5\left(CD-DQ\right)\Rightarrow5DQ=4CD\Rightarrow DQ=\dfrac{4}{5}CD\)
\(\Rightarrow\overrightarrow{DQ}=-\dfrac{4}{5}\overrightarrow{CD}\)
Ta có:
\(\overrightarrow{PQ}=\overrightarrow{PA}+\overrightarrow{AD}+\overrightarrow{DQ}=-\dfrac{4}{5}\overrightarrow{AB}+\overrightarrow{AD}-\dfrac{4}{5}\overrightarrow{CD}\)
\(=-\dfrac{4}{5}\left(\overrightarrow{AD}+\overrightarrow{DB}\right)+\overrightarrow{AD}-\dfrac{4}{5}\overrightarrow{CD}=-\dfrac{4}{5}\overrightarrow{AD}-\dfrac{4}{5}\overrightarrow{DB}+\overrightarrow{AD}-\dfrac{4}{5}\overrightarrow{CD}\)
\(=\dfrac{1}{5}\overrightarrow{AD}-\dfrac{4}{5}\left(\overrightarrow{CD}+\overrightarrow{DB}\right)=\dfrac{1}{5}\overrightarrow{AD}-\dfrac{4}{5}\overrightarrow{CB}\)
\(=\dfrac{1}{5}\overrightarrow{AD}+\dfrac{4}{5}\overrightarrow{BC}\)
Mà \(\overrightarrow{AD};\overrightarrow{BC}\) không cùng phương\(\Rightarrow\overrightarrow{AD};\overrightarrow{BC};\overrightarrow{PQ}\) đồng phẳng
DV
3
DV
2
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2022
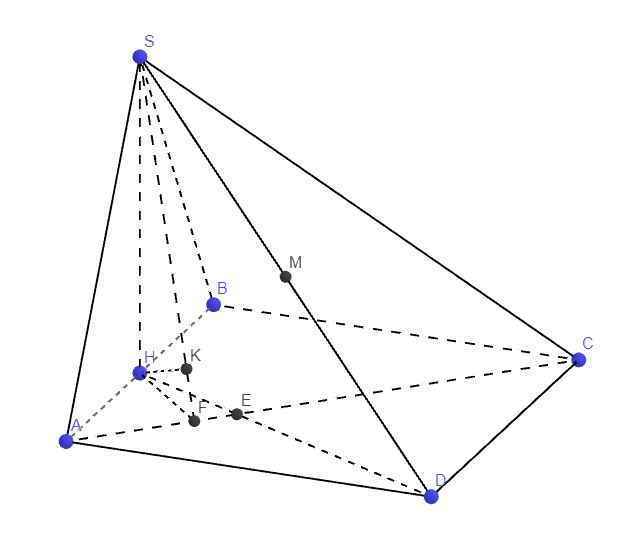
Gọi H là trung điểm AB, có lẽ từ 2 câu trên ta đã phải chứng minh được \(SH\perp\left(ABCD\right)\)
Do \(\left\{{}\begin{matrix}DM\cap\left(SAC\right)=S\\MS=\dfrac{1}{2}DS\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)\)
Gọi E là giao điểm AC và DH
Talet: \(\dfrac{HE}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow HE=\dfrac{1}{2}DE\)
\(\left\{{}\begin{matrix}DH\cap\left(SAC\right)=E\\HE=\dfrac{1}{2}DE\end{matrix}\right.\) \(\Rightarrow D\left(H;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)=d\left(M;\left(SAC\right)\right)\)
Từ H kẻ HF vuông góc AC (F thuộc AC), từ H kẻ \(HK\perp SF\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
ABCD là hình vuông \(\Rightarrow\widehat{HAF}=45^0\Rightarrow HF=AH.sin45^0=\dfrac{a\sqrt{2}}{4}\)
\(SH=\dfrac{a\sqrt{3}}{2}\), hệ thức lượng:
\(HK=\dfrac{SH.HF}{\sqrt{SH^2+HF^2}}=\dfrac{a\sqrt{21}}{14}\)
\(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{a\sqrt{21}}{14}\)
