Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

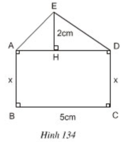
Ta có AD = BC = 5cm
Diện tích ΔADE: 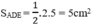
Diện tích hình chữ nhật ABCD: SABCD = 5x
Theo đề bài ta có SABCD = 3SADE ⇔ 5x = 3.5 ⇔ x = 3.
Vậy x = 3cm

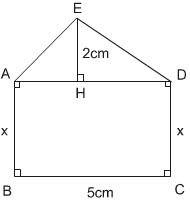
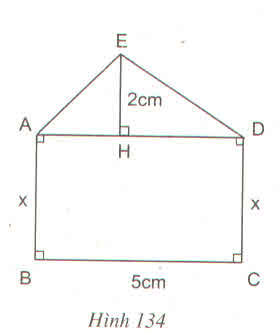
Ta có AD = BC = 5cm
Diện tích ∆ADE: SADE =  2.5 = 5(cm)
2.5 = 5(cm)
Diện tích hình chữ nhật ABCD: SABCD = 5x
Theo đề bài ta có
SABCD= 3SADE nên 5x = 3.5
Vậy x = 3cm

tam giácABC : MN là đường trung bình => MN// AC ,tam giác ADC có DP là đường trung bình => QP//AC ==> MN//QP(1) Xét r=tam giác BCD có NP là đường trung binh=> NP//BD=> GÓC MNP=90 ĐỘ(2) từ 1 và 2 => MNPQ là hình chữ nhật b) MNPQ/ABCD=1/2 C) diện tích ABCD=9.6/2=27 , diện tích MNPQ=27/2=13.5 diện tích MNB=3.375

Bạn tự vẽ hình nha ( hình nó dễ )
Gọi F là trung điểm của BC. Cắt hình thang theo đường DF đưa ghép vềnhư hình vẽ, điểm C trùng với điểm B , điểm D trùng với điểm E
Vì AB // CD \(\Rightarrow\)\(\widehat{ABC}+180\)độ \(\Leftrightarrow\)A ; B ; E thẳng hàng
\(\widehat{ABF}+\widehat{DFC}=180\)độ
\(\Rightarrow\)D ; F ; E thẳng hàng
\(\Delta DFC=\Delta EFB\left(g-c-g\right)\)
Diện tích DFC = diện tích EFB
\(\Rightarrow\)Diện tích ABCD = diện tích ADE
\(\Delta DFC=\Delta EFB\left(cmt\right)\)
DC = BE
AE = AB + BE = AB + CD
Diện tích ADE = \(\frac{1}{2}DH.AE=\frac{1}{2}DH.\left(AB+CD\right)\)
Vậy diện tích ABCD = \(\frac{1}{2}DH.AE=\frac{1}{2}DH.\left(AB+CD\right)\)