Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để chứng minh rằng EO là đường trung trực của AB trong hình thang cân ABCD, ta cần sử dụng một số kiến thức về hình học và các định lý liên quan.
Đầu tiên, do hình thang ABCD là hình thang cân, ta có AB // CD. Điều này có nghĩa là tam giác ABE và CDE là hai tam giác đồng dạng (có các cặp góc tương đồng và các cặp cạnh tương tỉ).
Tiếp theo, ta biết rằng đường chéo AC của hình thang cân là đường trung tuyến, có nghĩa là nó chia đôi đường chéo BD. Do đó, ta có AO = OC và BO = OD.
Giả sử EO không phải là đường trung trực của AB. Khi đó, ta có hai trường hợp xảy ra:
Trường hợp 1: EO nằm bên trong tam giác ABE. Trong trường hợp này, ta có EO cắt AB tại một điểm F. Vì tam giác ABE và CDE đồng dạng, nên ta cũng có EF // CD. Tuy nhiên, điều này mâu thuẫn với giả thiết AB // CD. Vậy trường hợp này không xảy ra.
Trường hợp 2: EO nằm bên ngoài tam giác ABE. Trong trường hợp này, ta có EO cắt AB tại một điểm F. Vì tam giác ABE và CDE đồng dạng, nên ta cũng có EF // CD. Tuy nhiên, điều này cũng mâu thuẫn với giả thiết AB // CD. Vậy trường hợp này cũng không xảy ra.
Vì hai trường hợp trên không xảy ra, ta kết luận rằng EO phải là đường trung trực của AB trong hình thang cân ABCD.
Hy vọng rằng giải thích trên đã giúp bạn hiểu và chứng minh được rằng EO là đường trung trực của AB trong hình thang cân ABCD.
Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
=>ΔABD=ΔBAC
=>góc OAB=góc OBA
=>OA=OB
Xét ΔEDC có AB//DC
nên EA/AD=EB/BC
mà AD=BC
nên EA=EB
mà OA=OB
nên EO là trung trực của AB

1.
O A B D C E
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB

Ta có: ∠(ADC) = ∠(BCD) (gt)
⇒ ∠(ODC) = ∠(OCD)
⇒ΔOCD cân tại O (dhnb tam giác cân)
⇒ OC = OD
OB + BC = OA + AD
Mà AD = BC (hình thang ABCD cân)
⇒ OA = OB
Xét ΔADC và. ΔBCD:
AD = BC (hình thang ABCD cân )
AC = BD (hình thang ABCD cân)
CD chung
Do đó ΔADC và ΔBCD (c.c.c)
⇒ ∠D1= ∠C1
⇒ΔEDC cân tại E (dhnb tam giác cân)
⇒ EC = ED nên E thuộc đường trung trực CD
OC = OD nên O thuộc đường trung trực CD
E ≠ O. Vậy OE là đường trung trực của CD.
Ta có: BD= AC (hình thang ABCD cân)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
Mà OA = OB (cmt)
Nên O thuộc đường trung trực của AB
E ≠ O. Vậy OE là đường trung trực của AB.
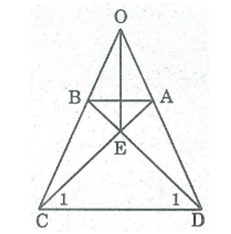
Để chứng minh rằng EO là đường trung trực của AB trong hình thang cân ABCD, chúng ta có thể sử dụng các điều kiện và tính chất của hình thang cân.
Vì hình thang ABCD là hình thang cân, nên ta có ab//cd và AD = BC.
Điều này cho phép chúng ta sử dụng các tính chất của các tam giác đồng dạng để chứng minh EO là đường trung trực của AB.
Ta có thể chứng minh rằng tam giác AEO và tam giác BEO đồng dạng bằng cách sử dụng góc và cạnh tương đồng.
Từ ab//cd, ta có: ∠AEO = ∠BEO (góc đối) ∠EAO = ∠EBO (góc đối)
Vì AD = BC, ta có: AE/BE = AD/BC = AO/BO (điều này được gọi là tỉ số phân giác)
Từ đó, ta có thể kết luận rằng tam giác AEO và tam giác BEO đồng dạng (góc và cạnh tương đồng).
Do đó, theo tính chất của các tam giác đồng dạng, ta biết rằng EO là đường trung trực của AB.
Vậy, ta đã chứng minh được rằng EO là đường trung trực của AB trong hình thang cân ABCD.
Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
=>ΔABD=ΔBAC
=>góc OAB=góc OBA
=>OA=OB
Xét ΔEDC có AB//DC
nên EA/AD=EB/BC
mà AD=BC
nên EA=EB
mà OA=OB
nên EO là trung trực của AB