Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

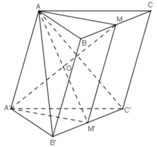
a) Do ABC.A’B’C’ là hình lăng trụ nên ta có: BCC’B’ là hình bình hành
Xét tứ giác BCC’B’ có M và M’ lần lượt là trung điểm của BC và B’C’ nên MM’ là đường trung bình
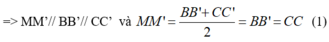
Lại có: AA’// BB’ và AA’= BB’ ( tính chất hình lăng trụ) (2)
Từ (1) và (2) suy ra: MM’// AA’ và MM’ = AA’
=> Tứ giác AMM’A’ là hình bình hành
b) Trong (AMM’A’) gọi O = A’M ∩ AM’, ta có :
Ta có : O ∈ AM’ ⊂ (AB’C’)
⇒ O = A’M ∩ (AB’C’).
c)
Gọi K = AB’ ∩ BA’, ta có :
K ∈ AB’ ⊂ (AB’C’)
K ∈ BA’ ⊂ (BA’C’)
⇒ K ∈ (AB’C’) ∩ (BA’C’)
Dễ dàng nhận thấy C’ ∈ (AB’C’) ∩ (BA’C’)
⇒ (AB’C’) ∩ (BA’C’) = KC’.
Vậy d cần tìm là đường thẳng KC’
d) Trong mp(AB’C’), gọi C’K ∩ AM’ = G.
Ta có: G ∈ AM’ ⊂ (AM’M)
G ∈ C’K.
⇒ G = (AM’M) ∩ C’K.
+ K = AB’ ∩ A’B là hai đường chéo của hình bình hành ABB’A’
⇒ K là trung điểm AB’.
ΔAB’C’ có G là giao điểm của 2 trung tuyến AM’ và C’K
⇒ G là trọng tâm ΔAB’C’.

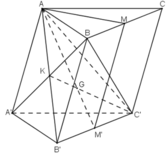
a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB', CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.
Nếu gọi Q là điểm trên cạnh BB' sao cho NQ // PM thì Q là giao điểm của đường thẳng BB' với mặt phẳng (MNP)
Nhận xét. Ta có thể tìm điểm Q bằng cách nối P với trung điểm I của đoạn MN và đường thẳng PI cắt BB' tại Q.
b) Vì mặt phẳng (AA', BB') song song với mặt phẳng (DD', CC') nên ta có MQ // PN. Do đó mặt phẳng (MNP) cắt hình hộp theo thiết diện MNPQ là một ình bình hành.
Giả sử P không phải là trung điểm của đoạn DD'. Gọi H = PN ∩ DC , K = MP ∩ AD. Ta có D = HK là giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Chú ý rằng giao điểm E = AB ∩ MQ cũng nằm trên giao tuyến d nói trên. Khi P là trung điểm của DD' mặt phẳng (MNP) song song với mặt phẳng (ABCD).

Ta có: ABB'A' là hình bình hành, M, N là trung điểm của AA', BB' nên MN // AB (đường trung bình) suy ra MN // (ABC).
Tương tự, ta có NP // BC suy ra NP// (ABC).
Mặt phẳng (MNP) chứa hai đường thẳng cắt nhau MN, NP và MN, NP song song với mp(ABC) suy ra (MNP) //(ABC).

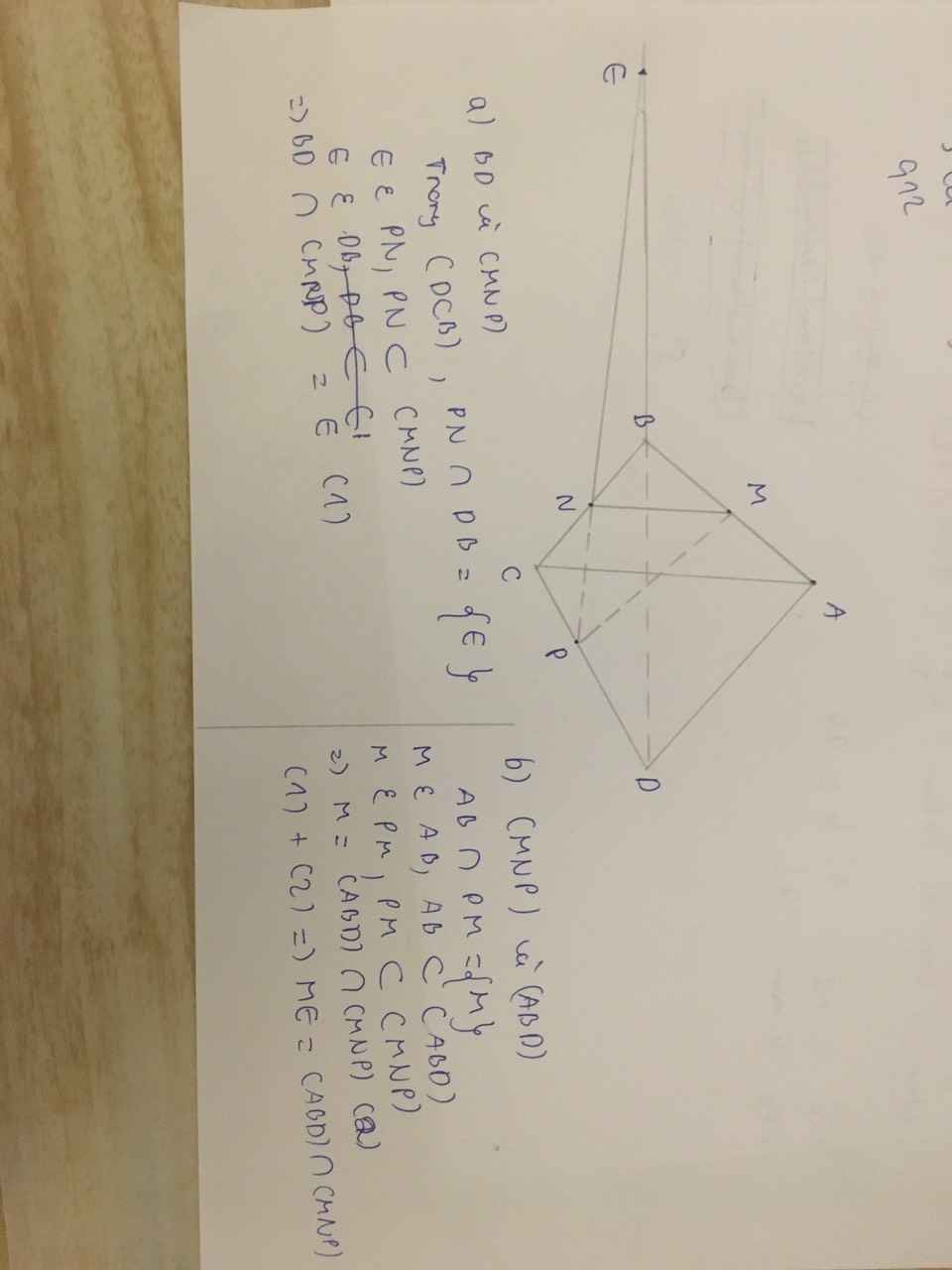
a) Ta có: MP cắt BC tại E mà BC thuộc (BCD)
Nên: E là giao điểm của đường thẳng MP với mặt phẳng (BCD).
b) Ta có: EN cắt CD tại Q mà EN thuộc (MNP)
Nên: Q là giao điểm của đường thẳng CD với mặt phẳng (MNP).
c) Ta có: P thuộc (MNP) và (ACD)
Q thuộc (MNP) và (ACD)
Nên PQ là giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
d) △ACN có: \(\dfrac{AP}{AC}=\dfrac{AG}{AN}=\dfrac{2}{3}\)
Suy ra: PG // CN
Do đó: △PIG đồng dạng với △NIC
Do đó: C, I, G thẳng hàng.

a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB',CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.


a) Gọi H là trung điểm của BC
△ABC có: E là trung điểm của AC, H là trung điểm của BC
Suy ra: EH // AB
Mà AB // A'B'
Do đó: EH // A'B' hay EH // B'F (1)
Ta có: EH // AB nên \(\dfrac{EH}{AB}=\dfrac{EC}{AC}=\dfrac{1}{2}\)
Mà AB = A'B', B'F = \(\dfrac{1}{2}\) A'B'
Nên: EH = B'F (2)
(1)(2) suy ra: EHB'F là hình bình hành. Do đó: EF // B'H
Mà B'H thuộc (BCC'B')
Suy ra: EF // (BCC'B')
b) Gọi K là trung điểm AB
Dễ dàng chứng minh được FKBB' là hình bình hành
Ta có: FK // BB'
Mà BB' // CC'
Suy ra: FK // CC' (1)
Ta có: FK = BB', mà BB' = CC'
Do đó: FK = CC' (2)
(1)(2) suy ra FKCC' là hình bình hành
Mà hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường
Nên C'K cắt CF tại trung điểm của hai đường thẳng
mà C'K thuộc (AC'B) , CF cắt (AC'B) tại I (đề bài)
Do đó: I là trung điểm của CF.
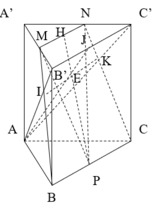

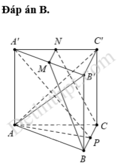
a) Ta có \(\left( {MNP} \right) \cap \left( {ABC} \right) = MN,\left( {ABC} \right) \cap \left( {ACC'A'} \right) = AC,AC//MN\) (do MN là đường trung bình của tam giác ABC) suy ra giao tuyến của (MNP) và (ACC'A') song song với MN và AC.
Qua P kẻ đường thẳng song song với AC cắt CC' tại H.
PH là giao tuyến của (MNP) và (ACC'A').
Nối H với N cắt B'C tại K.
Vậy K là giao điểm của (MNP) và B'C.
b) Gọi giao điểm BC' và B'C là O.
Ta có ACC'A' là hình bình hành P là trung điểm AA', PH //AC suy ra H là trung điểm CC'.
Xét tam giác CC'B ta có: HN là đường trung bình suy ra CK = OK.
Mà OC = OB' suy ra \(\frac{{KB'}}{{KC}} = 3\).