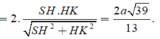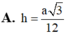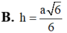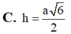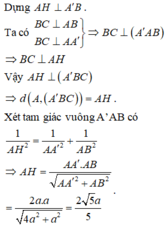Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nha mình biếng á chứ khog có j đou=)
Ta có : \(\left\{{}\begin{matrix}CA\perp AB\\\left(ABC\right)\perp\left(SAB\right)\\\left(ABC\right)\cap\left(SAB\right)=AB\end{matrix}\right.\) \(\Rightarrow CA\perp\left(SAB\right)\)
Kẻ \(AK\perp SB\) và \(AH\perp CK\) tại H.
Ta có : \(\left\{{}\begin{matrix}SB\perp AK\\SB\perp CA\end{matrix}\right.\) \(\Rightarrow SB\perp\left(ACK\right)\Rightarrow SB\perp AH\)
Do : \(\left\{{}\begin{matrix}AH\perp CK\\AH\perp SB\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\Rightarrow d\left(A;\left(SBC\right)\right)=AH\)
Xét t/g ABK , ta có : AK = AB
=> \(sin\widehat{ABK}=\alpha sin60^o=\dfrac{a\sqrt{3}}{2}\)
Xét t/g ACK , ta có : \(\dfrac{1}{AH^2}=\dfrac{1}{AK^2}+\dfrac{1}{AC^2}=\dfrac{7}{3a^2}\Rightarrow AH=\dfrac{a\sqrt{21}}{7}\)

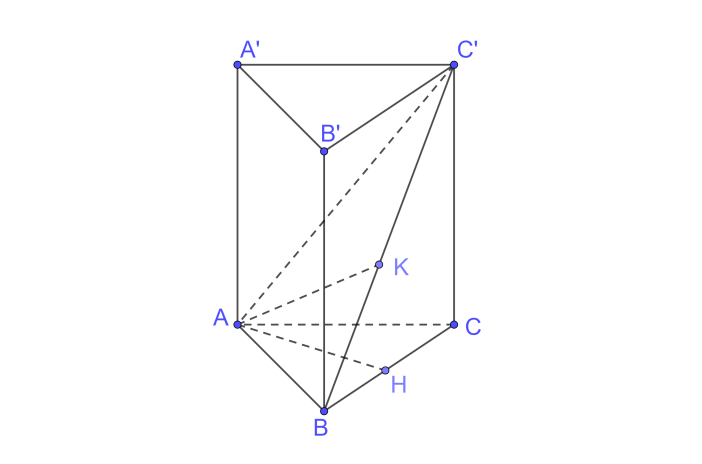
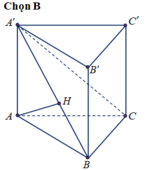
a) Ta có \(BB' \bot \left( {ABC} \right);BB' \subset \left( {BCC'B'} \right) \Rightarrow \left( {ABC} \right) \bot \left( {BCC'B'} \right)\)
\(\left( {ABC} \right) \cap \left( {BCC'B'} \right) = BC\)
(ABC): Kẻ \(AH \bot BC\)
\( \Rightarrow AH \bot \left( {BCC'B'} \right) \Rightarrow d\left( {A,\left( {BCC'B'} \right)} \right) = AH\)
Xét tam giác ABC vuông cân tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{2}{{{a^2}}}\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow AH = \frac{{a\sqrt 2 }}{2}\)
b) +) Ta có \(AB \bot AC,AB \bot AA'\left( {AA' \bot \left( {ABC} \right)} \right) \Rightarrow AB \bot \left( {ACC'A'} \right);AC' \subset \left( {ACC'A'} \right) \Rightarrow AC' \bot AB\)
Do đó tam giác ABC' là tam giác vuông.
+) Trên (ABC’) kẻ \(AK \bot BC' \Rightarrow d\left( {A,BC'} \right) = AK\)
Xét tam giác ACC’ vuông tại C có
\(A{C'^2} = A{C^2} + C{C'^2} = {a^2} + {h^2}\) (Định lí Pytago)
Xét tam giác ABC’ vuông tại A có
\(\begin{array}{l}\frac{1}{{A{K^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{{C'}^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2} + {h^2}}} = \frac{{2{a^2} + {h^2}}}{{{a^2}\left( {{a^2} + {h^2}} \right)}} \Rightarrow A{K^2} = \frac{{{a^2}\left( {{a^2} + {h^2}} \right)}}{{2{a^2} + {h^2}}}\\ \Rightarrow AK = a.\sqrt {\frac{{{a^2} + {h^2}}}{{2{a^2} + {h^2}}}} \end{array}\)

Ta có AA’//(BCC’B’) nên khoảng cách từ AA' đến mặt phẳng (BCC'B') cũng chính là khoảng cách từ A đến mặt phẳng (BCC'B').


1.
Gọi O là giao điểm AC và BD, Q là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\\OQ\perp AB\end{matrix}\right.\)
\(\Rightarrow AB\perp\left(SOQ\right)\)
Từ O kẻ \(OH\perp SQ\Rightarrow OH\perp\left(SAB\right)\Rightarrow OH=d\left(O;\left(SAB\right)\right)\)
\(OQ=\dfrac{BC}{2}=\dfrac{AB}{2}=\dfrac{a}{2}\) ; \(SO=\sqrt{SA^2-\left(\dfrac{BD}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\)
\(\dfrac{1}{OH^2}=\dfrac{1}{OQ^2}+\dfrac{1}{SO^2}=\dfrac{14}{3a^2}\Rightarrow OH=a\sqrt{\dfrac{14}{3}}\)
\(d\left(P;\left(SAB\right)\right)=2d\left(O;\left(SAB\right)\right)=2OH=2a\sqrt{\dfrac{14}{3}}\)
2.
Câu này đề đúng ko nhỉ? Vì thấy quá nhiều dữ kiện thừa thãi.
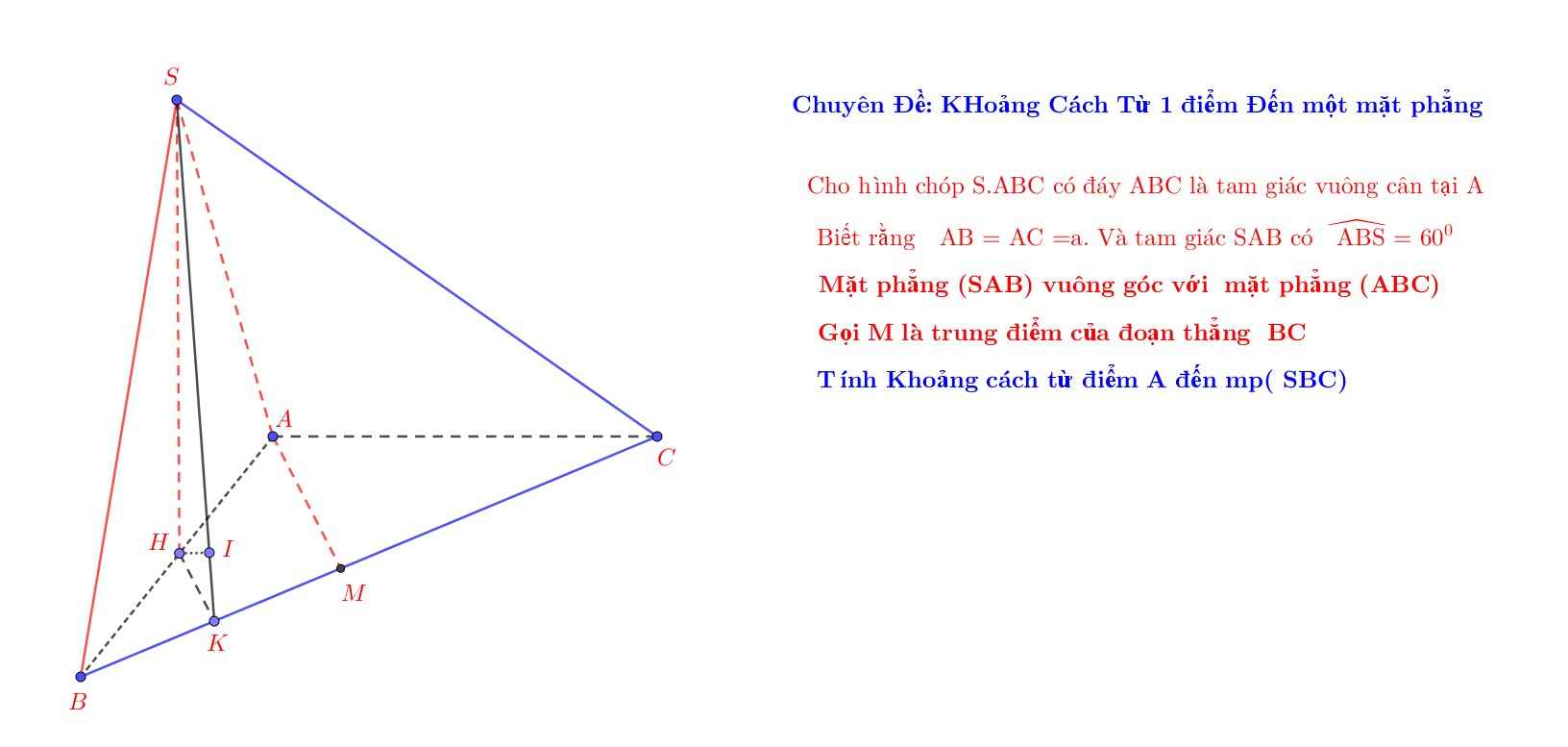
Từ \(\overrightarrow{IA}=-2\overrightarrow{IH}\Rightarrow I;A;H\) thẳng hàng
Mà ABC vuông cân tại A \(\Rightarrow AI\perp BC\Rightarrow AH\perp BC\)
Từ K kẻ \(KP||BC\) (P thuộc AH) \(\Rightarrow KP\perp AH\)
\(\left\{{}\begin{matrix}KP\in\left(SAB\right)\Rightarrow SH\perp KP\\KP\perp AH\end{matrix}\right.\) \(\Rightarrow KP\perp\left(SAH\right)\)
\(\Rightarrow KP=d\left(K;\left(SAH\right)\right)\)
\(KP=\dfrac{1}{2}IB\) (đường trung bình); \(IB=\dfrac{1}{2}BC=\dfrac{1}{2}AB\sqrt{2}=a\Rightarrow KP=\dfrac{a}{2}\)

Chọn C.
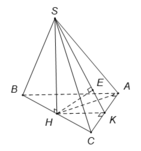
Gọi H là trung điểm của BC, suy ra .
![]()
Gọi K là trung điểm AC
![]()
![]()
![]()