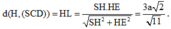Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

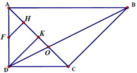
A N B C H K S
Theo giả thiết, \(HA=HC=\frac{1}{2}AC=a\) và \(SH\perp\left(ABC\right)\)
Xét \(\Delta v.ABC\) ta có : \(BC=AC.\cos\widehat{ACB}=2a\cos30^0=\sqrt{3}a\)
Do đó : \(S_{\Delta.ABC}=\frac{1}{2}AC.BC.\sin\widehat{ACB}=\frac{1}{2}.2a.\sqrt{3}a.\sin30^0=\frac{\sqrt{3}a^2}{2}\)
Vậy \(V_{S.ABC}=\frac{1}{3}SH.S_{ABC}=\frac{1}{3}.\sqrt{2}a.\frac{\sqrt{3}}{2}a^2=\frac{\sqrt{6}a^3}{6}\)
Vì CA=2HA nên d(C,(SAB))=2d(H, (SAB)) (1)
Gọi N là trung điểm của Ab, ta có HN là đường trung bình của tam giác ABC
Do đó HN//BC suy ra AB vuông góc với HN.
Lại có AB vuông góc với Sh nên AB vuông góc với mặt phẳng (SHN).
Do đó mặt phẳng (SAB) vuông góc với mặt phẳng (SHN).
Mà Sn là giao tuyến của 2 mặt phẳng vừa nêu, nên trong mặt phẳng (SHN), hạ HK vuông góc với SN, ta có HK vuông góc với mặt phẳng (SAB)
Vì vậy d(J, (SAB)) = HK. Kết hợp với (1), suy ra d(C. (SAB))=2HK (2)
Vì \(SH\perp\left(ABC\right)\) nên \(SH\perp HN\), xét tam giác v.SHN, ta có :
\(\frac{1}{HK^2}=\frac{1}{SH^2}+\frac{1}{HN^2}=\frac{1}{2a^2}+\frac{1}{HN^2}\)
Vì HN là đường trung bình của tam giác ABC nên \(HN=\frac{1}{2}BC=\frac{\sqrt{3}a}{2}\)
Do \(\frac{1}{HK^2}=\frac{1}{2a^2}+\frac{4}{3a^2}=\frac{11}{6a^2}\) suy ra \(HK=\frac{\sqrt{66}a}{11}\) (3)
Thế (3) vào (2) ta được \(d\left(C,\left(SAB\right)\right)=\frac{\sqrt{66}a}{11}\)

Chọn đáp án D
Ta có: HD là hình chiếu của SD lên mặt phẳng (ABCD).
Góc giữa SD và mặt phẳng (ABCD) là góc S D H ^ = 60 °
Kẻ HK
⊥
CD suy ra 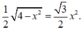
Góc giữa hai mặt phẳng (SCD) và (ABCD) là góc S K H ^ = α
Ta có: 
![]()

Mặt khác: HK//AD ![]()
![]()
Vậy: 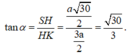
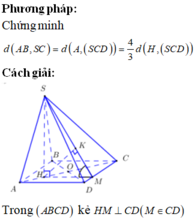
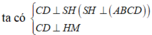
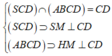
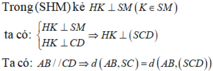
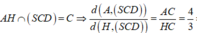

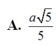
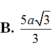
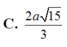
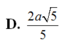
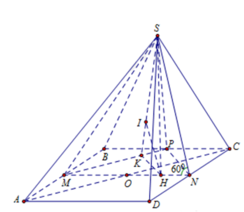
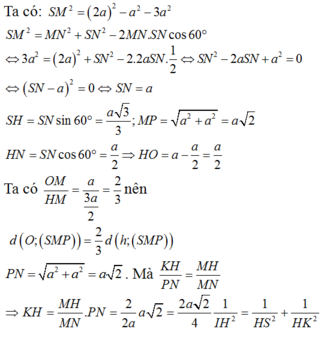
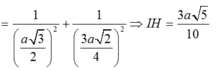
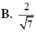
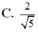
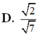
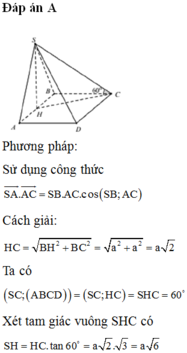
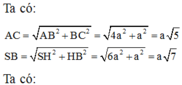
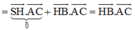
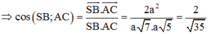
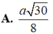
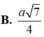
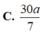
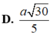

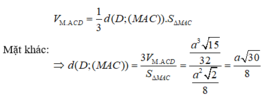

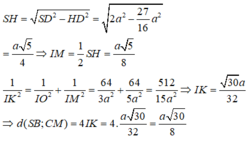
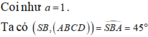


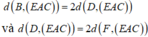
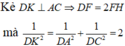

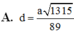
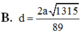
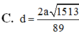
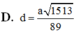

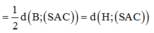

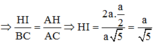
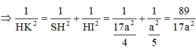
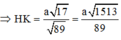
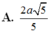
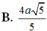
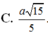
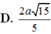
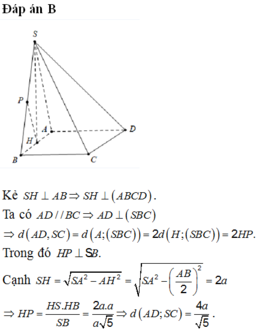
Phương pháp:
Sử dụng lí thuyết d(a,b) = d(a,(P)) = d(A,(P)), ở đó a,b chéo nhau, (P) chứa b và song song a và A ∈ a để tìm khoảng cách giữa hai đường thẳng SD, AB.
Tính khoảng cách và kết luận.
Cách giải:
Do AB//CD nên
Kẻ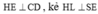
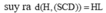
Ta có: SA = 2a,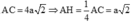
Khi đó