Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để đồ thị hàm số \(y=ax^2\) đi qua điểm A(4;4) thì
Thay x=4 và y=4 vào hàm số \(y=ax^2\), ta được:
\(a\cdot4^2=4\)
\(\Leftrightarrow a\cdot16=4\)
hay \(a=\dfrac{1}{4}\)
a, - Thay tọa độ điểm A vào hàm số ta được : \(4^2.a=4\)
\(\Rightarrow a=\dfrac{1}{4}\)
b, Thay a vào hàm số ta được : \(y=\dfrac{1}{4}x^2\)
- Ta có đồ thì của hai hàm số :
c, - Xét phương trình hoành độ giao điểm :\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy hai hàm số trên cắt nhau tại hai điểm : \(\left(0;0\right);\left(-2;1\right)\)

Bài 1.
Vì đths đi qua $M(-1;1)$ nên:
$y_M=2x_M+b$
$\Leftrightarrow 1=2.(-1)+b$
$\Leftrightarrow b=3$
Vậy đths có pt $y=2x+3$.
Hình vẽ:
Bài 2.
a. Hình vẽ:
Đường màu xanh là $y=2x-1$
Đường màu đỏ là $y=-x+2$
b.
PT hoành độ giao điểm:
$y=2x-1=-x+2$
$\Leftrightarrow x=1$
$y=2x-1=2.1-1=1$
Vậy tọa độ giao điểm của 2 đồ thị là $(1;1)$

mình giải bên 24 rồi nhé, đths thì bạn tự vẽ
1, đths y = 2x + b đi qua M(-1;1) <=> -2 + b = 1 <=> b = 3
2b, Hoành độ giao điểm thỏa mãn phương trình
2x - 1 = -x + 2 <=> 3x = 3 <=> x = 1
=> y = 2 - 1 = 1
Vậy y = 2x - 1 cắt y = -x +2 tại A(1;1)

a)
- Vẽ đường thẳng y = -x + 6
Cho x = 0 ⇒ y = 6 được điểm (0, 6)
Cho y = 0 ⇒ x = 6 được điểm (6, 0)
⇒ Đường thẳng y = -x + 6 đi qua các điểm (6; 0) và (0; 6).
- Lập bảng giá trị và vẽ đồ thị hàm số 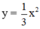
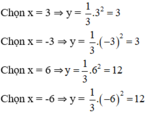
⇒ Parabol đi qua các điểm (3; 3); (-3; 3); (-6; 12); (6; 12); (0; 0).
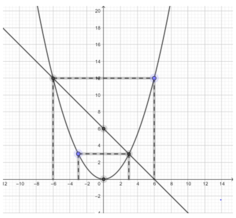
b)Xét phương trình hoành độ giao điểm


PT hoành độ giao điểm của (p) và (d) là:
x\(^2\)=x+2
=>x\(^2\)-x -2=0
Ta có: a=1,b=-1, c=-2:a-b+c=0
=>pt có 2no pb x1=-1 x 2=2
Thay x vào tìm y