Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thu gọn rồi tính giá trị của đa thức P tại x = 0,5 và y = 1:


Cái bài này mình đã từng đăng để hỏi mấy bạn kia.
Nhưng đề câu này thiểu bạn ơi.
Phải có x=a/m ; y=b/m
À thôi, mk viết đầy đủ đề thử nhé !
Giả sử:x=a/m;y=b/m (a,b,m thuộc Z.m > 0) và x < y.
Hãy chứng minh (chứng tỏ) rằng nếu chọn z=a+b/2m thì ta có x < y < z.
Trong sách lớp 7 đề y như z đó !
Mk ghi cách làm luôn nha !
Giả sử x=a/m,y=b/m (a,b,m thuộc Z,m > 0 )
Vì x < y nên ta suy ra a < b.
ta có: x=a/m, y=b/m <=> x=2a/am. y=2b/2m
mà a < b nên a+a < a+b <=> 2a < a+b
Do 2a < a+b thì x < y ( 1 )
Ta lại có: a < b nên a+b < b+b <=> a+b < 2b
Mà a+b < 2b <=> x < z ( 2 )
Từ ( 1 ) và ( 2 ) suy ra x < y < z (ĐPCM)

a: Ta có: \(P=x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)
\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
Ta có: \(Q=5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
\(=-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)


a) Sắp xếp theo lũy thừa giảm dần
P(x)=x^5−3x^2+7x^4−9x^3+x^2−1/4x
=x^5+7x^4−9x^3−3x^2+x^2−1/4x
=x^5+7x^4−9x^3−2x^2−1/4x
Q(x)=5x^4−x^5+x^2−2x^3+3x^2−1/4
=−x^5+5x^4−2x^3+x^2+3x^2−1/4
=−x^5+5x^4−2x^3+4x^2−1/4
b)
P(x)+Q(x)
=(x^5+7x^4−9x^3−2x^2−1/4^x)+(−x^5+5x^4−2x^3+4x^2−1/4)
=x^5+7x^4−9x^3−2x^2−1/4x−x^5+5x^4−2x^3+4x^2−1/4
=(x^5−x^5)+(7x^4+5x^4)+(−9x^3−2x^3)+(−2x^2+4x^2)−1/4x−1/4
=12x^4−11x^3+2x^2−1/4x−1/4
P(x)−Q(x)
=(x^5+7x^4−9x^3−2x^2−1/4x)−(−x^5+5x^4−2x^3+4x^2−1/4)
=x^5+7x^4−9x^3−2x^2−1/4x+x^5−5x^4+2x^3−4x^2+1/4
=(x^5+x^5)+(7x^4−5x^4)+(−9x^3+2x^3)+(−2x^2−4x^2)−1/4x+1/4
=2x5+2x4−7x3−6x2−1/4x−1/4
c) Ta có
P(0)=0^5+7.0^4−9.0^3−2.0^2−1/4.0
⇒x=0là nghiệm của P(x).
Q(0)=−0^5+5.0^4−2.0^3+4.0^2−1/4=−1/4≠0
⇒x=0không phải là nghiệm của Q(x).
Cho 2 đa thức: f(x)= 9 - x5 + 4x - 2x3 + x2 - 7x4
g(x)= x5 - 9 + 2x2 + 7x4 + 2x3 - 3x
a) Sắp sếp các đa thức trên theo luỹ thừa giảm dần của biến
f(x)= 9 - x5 + 4x - 2x3 + x2 - 7x4
f(x) = -x5 - 7x4 - 2x3 + x2 + 4x + 9
g(x)= x5 - 9 + 2x2 + 7x4 + 2x3 - 3x
g(x) = x5 + 7x4 + 2x3 + 2x2 - 3x - 9
b) Tìm bậc, hệ số cao nhất, hệ số tự do của đa thức f(x); g(x)
f(x) = -x5 - 7x4 - 2x3 + x2 + 4x + 9
+ Bậc : 5 _ hệ số cao nhất : -1 _ hệ số tự do : 9
g(x) = x5 + 7x4 + 2x3 + 2x2 - 3x - 9
+ Bậc : 5_ hệ số cao nhất : 1 _ hệ số tự do : -9
c) Tính f(x) + g(x); f(x) - g(x)
f( x) + g(x) = ( -x5 - 7x4 - 2x3 + x2 + 4x + 9 ) +( x5 + 7x4 + 2x3 + 2x2 - 3x - 9 )
= -x5 - 7x4 - 2x3 + x2 + 4x + 9 + x5 + 7x4 + 2x3 + 2x2 - 3x - 9
= ( -x5 + x5 ) + ( -7x4 + 7x4 ) + ( -2x3 + 2x3 ) + ( x2 + 2x2 ) + ( 4x -3x ) + ( 9 - 9 )
= 3x2 + x
f( x) - g(x) = ( -x5 - 7x4 - 2x3 + x2 + 4x + 9 ) - ( x5 + 7x4 + 2x3 + 2x2 - 3x - 9 )
= -x5 - 7x4 - 2x3 + x2 + 4x + 9 - x5 - 7x4 - 2x3 - 2x2 + 3x + 9
= ( -x5 - x5 ) + ( -7x4 - 7x4 ) + ( -2x3 - 2x3 ) + ( x2 - 2x2 ) + ( 4x + 3x ) + ( 9 + 9 )
= -2x5 - 14x4 - 2x3 -x2 + 7x + 18
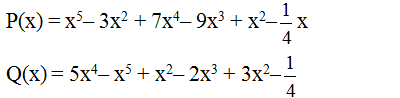
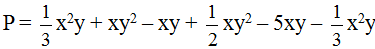
 (a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 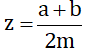 thì ta có x < z < y.
thì ta có x < z < y.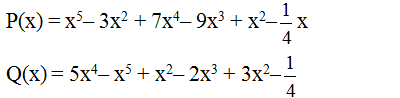



a) Ta có: M(x) = 5x3 + 2x4 – x2 + 3x2 – x3 – x4 + 1 – 4x3 = x4 + 2x2 + 1 b) Ta có (M1) = 14 + 2.12 + 1 = 1 + 2 + 1 = 4 và (M-1) = (-1)4 + 2.(-1)2 + 1 + 1 + 2 + 1 = 4 c) Ta có M(x) = x4 + 2x2 + 1 = (x2+1)2 Nhận xét: Vì x2 ≥ 0 => x2 + 1 > 1 => (x2 + 1)2 > 1 > 0 với mọi x ∈ R Vậy M(x) = (x2 +1)2 > 0 với mọi x ∈ R. Điều này chứng tỏ rằng M(x) không có nghiệm trong R.
Bạn ơi phần nào có số đằng sau x là mũ nhé! ko biết ấn dấu mũ
Bài thế mà cũng hỏi! Bạn phải suy nghĩ trước đã chứ!!!