Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương trình hoành độ giao điểm của đường cong y = tan x trục hoành là tan x = 0 ⇔ x = k π
V = π ∫ 0 π 4 tan 2 x d x = π ∫ 0 π 4 1 cos 2 x - 1 d x = π tanx - x 0 π 4 = π 1 - π 4

Đáp án D.
Thể tích V của khối tròn xoay cần tính
V H = π . ∫ 0 1 f 2 x d x = π . ∫ 0 1 x . e 2 x 2 d x .
Đặt
t = e 2 x 2 ⇔ d t = 2 x 2 ' e 2 x 2 d x = 4 x . t d x ⇔ x d x = d t 4 t
và đổi cận x = 0 → t = 1 x = 1 → t = e 2 .
Khi đó V H = π ∫ 1 e 2 t . d t 4 t = π 4 ∫ 1 e 2 d x = π 4 e 2 − 1 .

Đáp án D
Phương trình hoành độ giao điểm x e x 2 = 0 ⇔ x = 0 ⇒ V = π ∫ 0 1 xe 2 x 2 d x = 1 4 π e 2 - 1 .

Đáp án D
Hoành độ giao điểm của đồ thị hàm số y = 4 x - a e 2 x và trục hoành nghiệm của phương trình
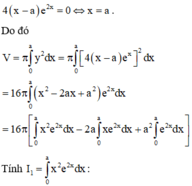
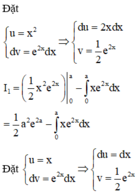
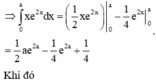
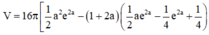
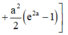
![]()
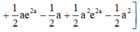
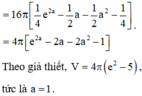

Đáp án B
V = π ∫ 1 2 [ ( − e x + 4 x ) ] 2 d x = π ∫ 1 2 ( 4 x − e x ) d x
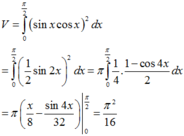
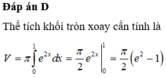


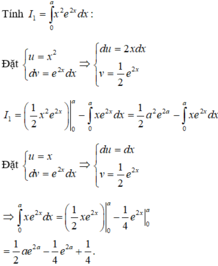
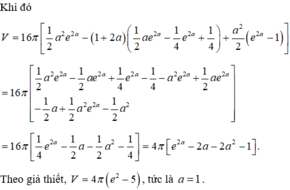
Chọn đáp án A
Thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox là:
Xét phương trình y 2 = a ⇔ y = ± a . Khi đó thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Oy là
Suy ra V 1 - V 2 8 = π 20 . a 2 10 - 4 a
Dấu “=” xảy ra khi và chỉ khi a = 10 - 4 a ⇔ a = 4 = a 0 (thỏa mãn).
Khi đó ∆ V = π 20 . 32 = 8 π 5
Vậy 5 ∆ = 2 πa 0