Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC

1, Vì MA ; MB lần lượt là tiếp tuyến (O) với A;B là tiếp điểm
=> ^MAO = ^MBO = 900
Xét tam giác MAOB có ^MAO + ^MBO = 1800
mà 2 góc đối Vậy tứ giác MAOB là tứ giác nt 1 đường tròn
2, Xét tam giác MAC và tam giác MDA
^M _ chung
^MAC = ^MDA ( cùng chắn cung AC )
Vậy tam giác MAC ~ tam giác MDA (g.g)
\(\dfrac{MA}{MD}=\dfrac{MC}{MA}\Rightarrow MA^2=MD.MC\)
3, Ta có AM = MB ( tc tiếp tuyến cắt nhau )
OB = OA = R
Vậy MO là đường trung trực
Xét tam giác MAO vuông tại A, đường cao AH
AO^2 = OH . OM ( hệ thức lượng )
\(\Rightarrow OM.OH+MC.MD=AO^2+AM^2=OM^2\left(pytago\right)\)

a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp đường tròn đường kính MO
Tâm là trung điểm của MO
Bán kính là MO/2
b: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB
góc ABK=1/2*sđ cung AK=90 độ
=>AB vuông góc BK
=>BK//OM
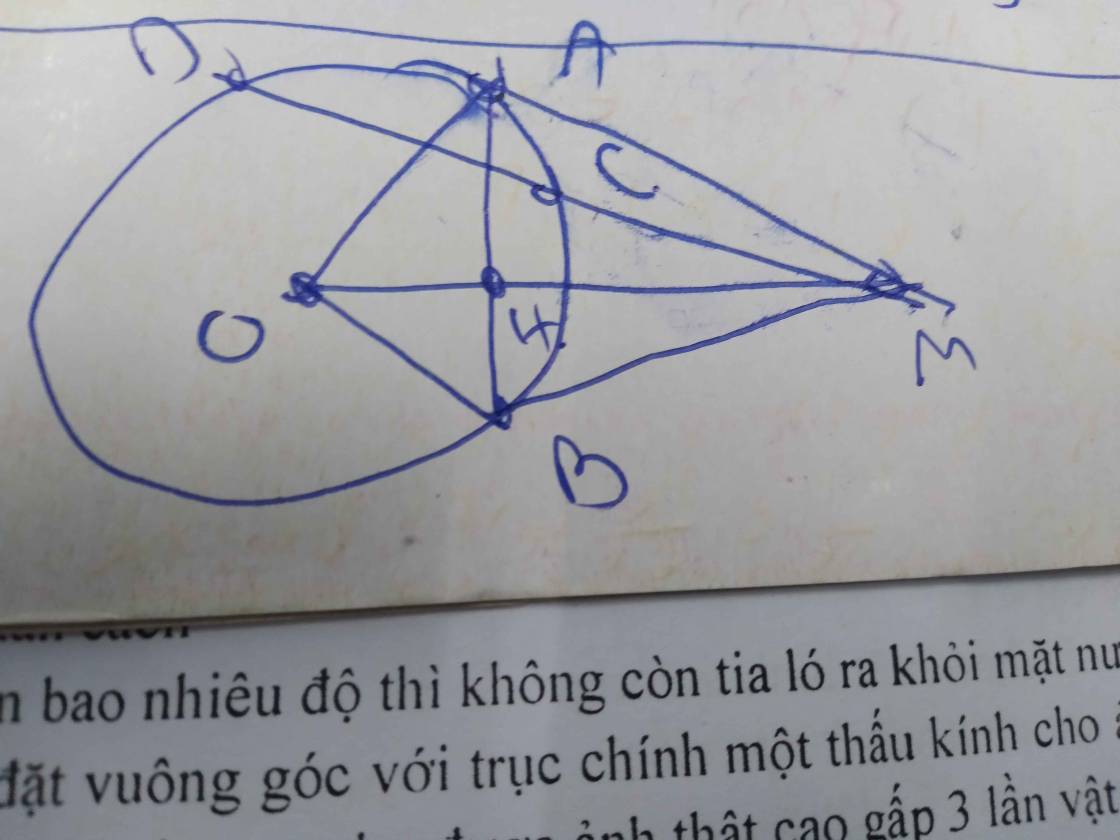

a.
Do MA là tiếp tuyến \(\Rightarrow MA\perp OA\)
\(\Rightarrow M,A,O\) cùng thuộc đường tròn đường kính OM
Do MB là tiếp tuyến \(\Rightarrow MB\perp OB\)
\(\Rightarrow M,B,O\) cùng thuộc đường tròn đường kính OM
\(\Rightarrow\) Tứ giác MAOB nội tiếp đường tròn đường kính OM
Do OM là đường kính nên tâm đường tròn là trung điểm OM.
b.
Do MAOB nội tiếp \(\Rightarrow\widehat{AOB}+\widehat{AMB}=180^0\)
\(\Rightarrow\widehat{AMB}=180^0-120^0=60^0\) (1)
Lại có M là giao điểm 2 tiếp tuyến tại A và B
\(\Rightarrow MA=MB\)
\(\Rightarrow\Delta AMB\) cân tại M (2)
(1);(2) \(\Rightarrow\Delta AMB\) đều (tam giác cân có 1 góc bằng 60 độ)
c.
Xét hai tam giác MAC và MDA có:
\(\left\{{}\begin{matrix}\widehat{AMC}\text{ chung}\\\widehat{MAC}=\widehat{MDA}\left(\text{cùng chắn AC}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MAC\sim\Delta MDA\left(g.g\right)\)
\(\Rightarrow\dfrac{MA}{MD}=\dfrac{MC}{MA}\Rightarrow MC.MD=MA^2\)