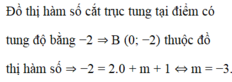Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2 suy ra điểm A(0; -2) thuộc đồ thị hàm số hay -2 = 2.0 + m + 1 suy ra m = -3
Chọn A.
A) Để đồ thị đi qua điểm M(-1, 1) thì thay x = -1, y = 1 vào hàm số ta có:
1 = (2m-1).(-1) + m + 1
=> m = 1
B) Hàm số đã cho là hàm bậc nhất, đồ thị là đường thẳng nên không thể đồ thị cắt trục hoành tại hai điểm được
a)y=(2m-1)x+m+1
Đồ thị hàm số đi qua điểm M(-1;1) khi và chỉ khi
1=(2m-1)(-1)+m+1
Giải phương trình ẩn m, tìm được: m=1
b)y=(2m-1)x+m+1
Cho x=0⇒y=m+1⇒A(0; m+1 ) ⇒OA =\(\left|m+1\right|\)
Cho y =0 ⇒x =\(\frac{-m-1}{2m-1}\Rightarrow B\left(\frac{-m-1}{2m-1};0\right)\)
\(\Rightarrow OB=\left|\frac{-m-1}{2m-1}\right|=\frac{\left|m+1\right|}{\left|2m-1\right|}\)
△AOB cân ⇔\(\left\{{}\begin{matrix}OA=OB\\OA>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left|m+1\right|=\frac{\left|m+1\right|}{\left|2m-1\right|}\\\left|m+1\right|>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left|2m-1\right|=1\\m\ne-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m-1=1\\2m-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)
Vậy với m = 0 hoặc m = 1 thì đồ thị hàm số thỏa mãn yêu cầu của bài toán
a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2
a/ Giao điểm với trục tung: thay \(x=0\)
\(\Rightarrow y=\frac{m}{-m}\)
Để đồ thị ko cắt Oy \(\Rightarrow\)y ko tồn tại \(\Leftrightarrow m=0\)
b/ Giao điểm với trục hoành: \(y=0\)
\(\Rightarrow\frac{x^2-mx+m}{x-m}=0\) vô nghiệm
- TH1: \(x^2-mx+m=0\) vô nghiệm
\(\Leftrightarrow\Delta=m^2-4m< 0\Rightarrow0< m< 4\)
TH2: \(x^2-mx+m=0\) có nghiệm \(x=m\)
\(\Leftrightarrow m^2-m^2+m=0\Rightarrow m=0\)
Vậy \(0\le m< 4\)
c/ Từ câu trên ta có \(m^2-4m>0\Rightarrow\left[{}\begin{matrix}m>4\\m< 0\end{matrix}\right.\)
Khi m = 2 : y = x + 5
TXĐ : D = R.
Tính biến thiên :
- a = 1 > 0 hàm số đồng biến trên R.
bảng biến thiên :
x | -∞ | +∞ | |
y | -∞ |
| +∞ |
Bảng giá trị :
x | 0 | -5 |
y | 5 | 0 |
Đồ thị hàm số y = x + 5 là đường thẳng đi qua hai điểm A(0, 5) và B(-5; 0).
b/(dm) đi qua điểm A(4, -1) :
4 = (m -1)(-1) +2m +1
<=> m = 2
3. hàm số nghịch biến khi : a = m – 1 < 0 <=> m < 1
4.(dm) đi qua điểm cố định M(x0, y0) :
Ta được : y0 = (m -1)( x0) +2m +1 luôn đúng mọi m.
<=> (x0 + 2) m = y0 – 1 + x0(*)
(*) luôn đúng mọi m khi :
x0 + 2= 0 và y0 – 1 + x0 = 0
<=> x0 =- 2 và y0 = 3
Vậy : điểm cố định M(-2, 3)