Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu M không là giao điểm của AC và BD thì MA+MC>AC; MB+MD>BD
=>MA+MB+MC+MD>AC+BD(1)
Nếu M là giao điểm của AC và BD thì MA+MB+MC+MD=AC+BD(2)
Từ (1) và (2) suy ra MA+MB+MC+MD>=AC+BD
Dấu '=' xảy ra khi M là giao điểm của AC và BD

Ta có: \(\left|MA-MB\right|\ge0\) với một điểm M tùy ý.
\(\left|MA-MB\right|=0\) chỉ với điểm M mà MA = MB
=> M nằm trên đường trung trực của đoạn thẳng AB. (Có giao điểm này vì AB không vuông góc với đường thẳng d)
Vậy, \(\left|MA-MB\right|\) đạt GTNN là 0 khi M là giao điểm của đường thẳng d và đường trung trực của đoạn thẳng AB.

Goi O là giao điểm 2 đường chéo AC và BD.
Lay điểm M bat ky ta luôn có:
MA + MC >= AC (1)
MB + MD >= BD (2)
=> MA + MB + MC + MD >= AC + BD khong doi
=> Min (MA + MB + MC + MD) = AC + BD xảy ra khi đồng thời xảy ra dấu = ở (1) <=> M thuộc AC và dấu = ở (2) <=> M cũng thuộc BD <=> M trùng O

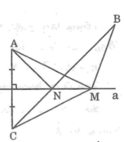
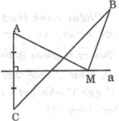
Theo chứng minh trên, khi M trùng với N thì MA + MB = BC bé nhất. Vậy khi M là giao điểm của BC với đường thẳng a thì MA + MB bé nhất.
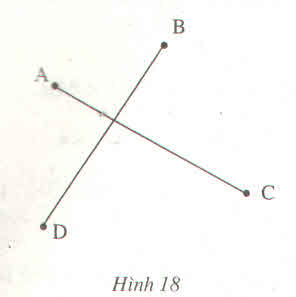
* Nếu M không trùng với giao điểm của AC và BD
Trong ΔAMC, ta có: MA + MC > AC (bất đẳng thức tam giác)
Trong ΔMBD, ta có: MB + MD > BD (bất đẳng thức tam giác)
* Nếu M trùng với giao điểm AC và BD
Ta có: MA + MC = AC
MB + MD = BD
+) Kết hợp cả hai trường hợp, suy ra: MA + MC ≥ AC
Và MB + MD ≥ BD (dấu bằng xảy ra khi M trùng với giao điểm của AC và BD)
Suy ra: MA + MB + MC + MD ≥ AC + BD
Vậy MA + MB + MC + MD = AC + BD bé nhất khi đó M là giao điểm của AC và BD.