K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 8 2021
a: Ta có: \(a+b+c=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=-c\\a+c=-b\\b+c=-a\end{matrix}\right.\)
Ta có: a+b+c=0
\(\Leftrightarrow\left(a+b+c\right)^3=0\)
\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(a+c\right)\left(b+c\right)=0\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow a^3+b^3+c^3=3abc\)
b: Ta có: \(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)
\(\Leftrightarrow a+b+c=0\)
21 tháng 8 2021
a) \(a^3+b^3+c^3=3abc\Leftrightarrow\left(a+b\right)^3+c^3-3a^2b-3ab^2-3abc=0\Leftrightarrow\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)(đúng do a+b+c = 0)
21 tháng 8 2021
a: Ta có: a+b+c=0
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=-c\\a+c=-b\\b+c=-a\end{matrix}\right.\)
Ta có: a+b+c=0
\(\Leftrightarrow\left(a+b+c\right)^3=0\)
\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(a+c\right)=0\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow a^3+b^3+c^3=3abc\)
b: Ta có: \(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)
\(\Leftrightarrow a+b+c=0\)
AH
Akai Haruma
Giáo viên
29 tháng 6 2023
Bài 1:
$a^3+b^3+c^3=3abc$
$\Leftrightarrow (a+b)^3-3ab(a+b)+c^3-3abc=0$
$\Leftrightarrow [(a+b)^3+c^3]-[3ab(a+b)+3abc]=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2]-3ab(a+b+c)=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2-3ab]=0$
$\Leftrightarrow (a+b+c)(a^2+b^2+c^2-ab-bc-ac)=0$
$\Rightarrow a+b+c=0$ hoặc $a^2+b^2+c^2-ab-bc-ac=0$
Xét TH $a^2+b^2+c^2-ab-bc-ac=0$
$\Leftrightarrow 2(a^2+b^2+c^2)-2(ab+bc+ac)=0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$
$\Rightarrow a-b=b-c=c-a=0$
$\Leftrightarrow a=b=c$
Vậy $a^3+b^3+c^3=3abc$ khi $a+b+c=0$ hoặc $a=b=c$
Áp dụng vào bài:
Nếu $a+b+c=0$
$A=\frac{-c}{c}+\frac{-b}{b}+\frac{-a}{a}=-1+(-1)+(-1)=-3$
Nếu $a=b=c$
$P=\frac{a+a}{a}+\frac{b+b}{b}+\frac{c+c}{c}=2+2+2=6$
PT
1
CM
23 tháng 10 2017
+) Ta có: a 3 + b 3 = a + b 3 - 3 a b a + b
Thật vậy, VP = a + b 3 – 3ab (a + b)
= a 3 + 3 a 2 b + 3 a b 2 + b 3 - 3 a 2 b - 3 a b 2
= a 3 + b 3 = VT
Nên a 3 + b 3 + c 3 = a + b 3 - 3 a b a + b + c 3 (1)
Ta có: a + b + c = 0 ⇒ a + b = - c (2)
Thay (2) vào (1) ta có:
a 3 + b 3 + c 3 = - c 3 - 3 a b - c + c 3 = - c 3 + 3 a b c + c 3 = 3 a b c
Vế trái bằng vế phải nên đẳng thức được chứng minh.
3 tháng 1 2022
\(\Leftrightarrow a^3+b^3+c^3-3abc>=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc>=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)>=0\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac>=0\)(vì a+b+c>0)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2>=0\)(luôn đúng)
3 tháng 1 2022
\(a^3+b^3+c^3\ge3abc\\ \Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc\ge0\\ \Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\ge0\\ \Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\ge0\)
Vì \(a,b,c>0\Leftrightarrow a+b+c>0\)
Lại có \(a^2+b^2+c^2-ab-bc-ca=\dfrac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\ge0\)
Nhân vế theo vế ta được đpcm
Dấu \("="\Leftrightarrow a=b=c\)
PT
2
VT
21 tháng 12 2021
a3+b3+c3= (a+b)3-3ab(a+b)+c3
Thay a+b=-c vào, ta được:
a3 + b3 +c3 = (-c)3 -3ab(-c) +c3 = 3abc (đpcm)
CM
24 tháng 12 2017
Ta có
( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 = a 3 + b 3 + 3 a b ( a + b ) = > a 3 + b 3 = ( a + b ) 3 – 3 a b ( a + b )
Từ đó
B = a 3 + b 3 + c 3 – 3 a b c = ( a + b ) 3 – 3 a b ( a + b ) + c 3 – 3 a b c = [ ( a + b ) 3 + c 3 ] – 3 a b ( a + b + c ) = ( a + b + c ) [ ( a + b ) 2 – ( a + b ) c + c 2 ] – 3 a b ( a + b + c )
Mà a + b + c = 0 nên
B = 0 . [ ( a + b ) 2 – ( a + b ) c + c 2 ] – 3 a b . 0 = 0
Vậy B = 0
Đáp án cần chọn là: A
PT
1
CM
7 tháng 5 2018
Ta có: a + b + c = 0
⇒ a + b = -c ⇒ (a + b)3 = (-c)3
⇒ a3 + b3 + 3ab(a + b) = -c3 ⇒ a3 + b3 + 3ab(-c) + c3 = 0
⇒ a3 + b3 + c3 = 3abc
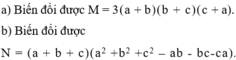
có:a+b+c=0 suy ra :a+b= -c(1)
(a+b)^3= -c^3
a^3+3a^2b+3ab^2+3b^3+c^3=0
a^3+b^3+c^3+3ab(a+b)=0
a^3+b^3+c^3-3abc=0(Vì a+b= -c)
a^3+b^3+c^3 =3abc