Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: Tham khảo:
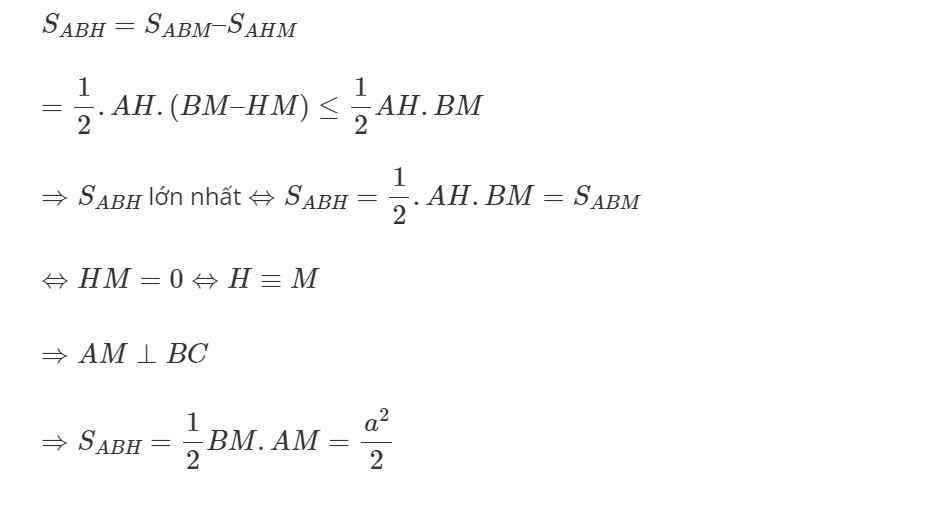
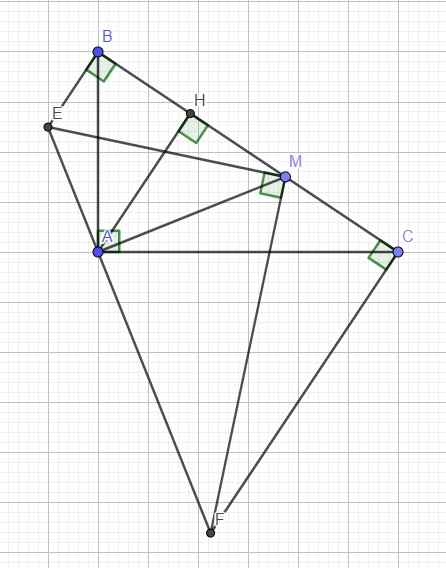
a: Ta có: góc MAB+góc PAB=90 độ
góc MBA+góc PBA=90 độ
mà góc MAB=góc MBA
nên góc PAB=góc PBA
=>PA=PB
Ta có: góc QAC+góc MAC=90 độ
góc QCA+góc MCA=90 độ
mà góc MAC=góc MCA
nên góc QAC=góc QCA
=>QA=QC

1c (2 câu kia em tự giải)
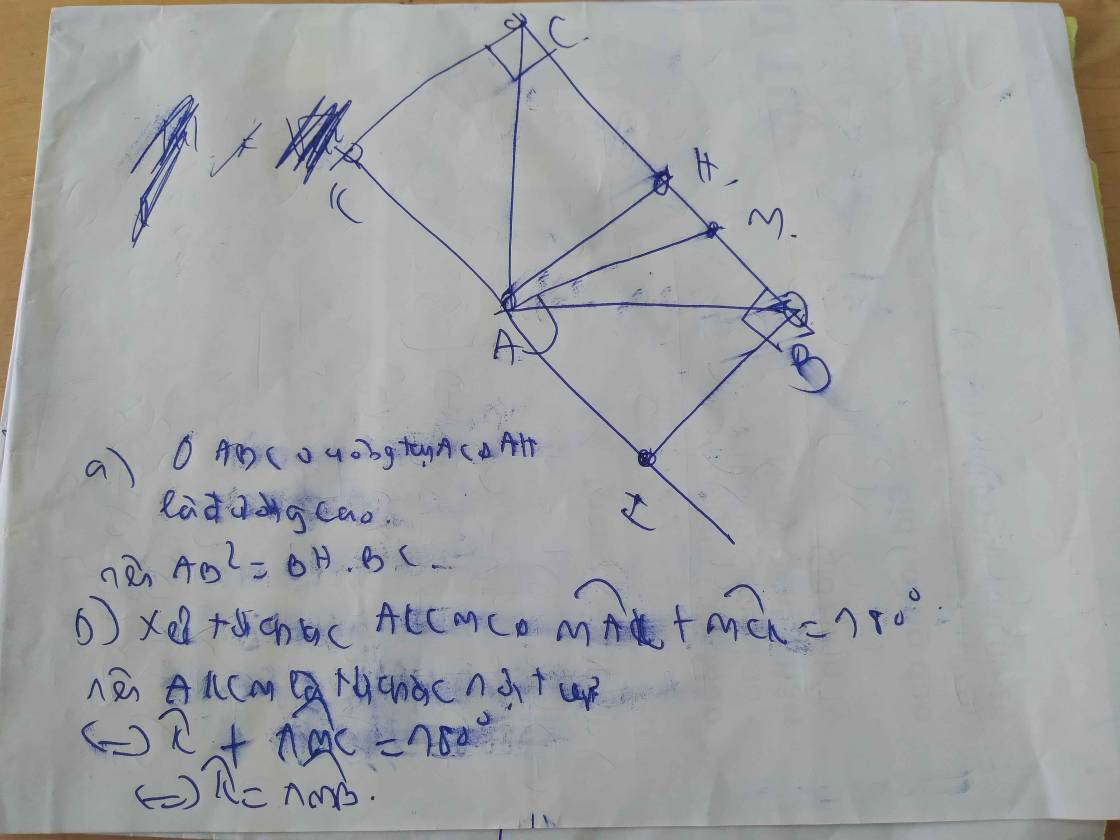
Kẻ đường cao AH \(\Rightarrow\) AH cố định
Do \(\widehat{MAF}\) và \(\widehat{MCF}\) cùng nhìn MF dưới 1 góc vuông nên tứ giác MAFC nội tiếp
\(\Rightarrow\widehat{AFM}=\widehat{ACM}\) (cùng chắn AM)
\(\Rightarrow\Delta_VFME\sim\Delta_VCAB\left(g.g\right)\) với tỉ số đồng dạng \(k=\dfrac{AM}{AH}\)
\(\Rightarrow S_{MEF}=k^2.S_{ABC}\Rightarrow S_{MEF-min}\) khi \(k_{min}\)
Mà trong tam giác vuông AHM ta có \(AH\le AM\Rightarrow k\ge1\Rightarrow k_{min}=1\) khi M trùng H
Hay diện tích MEF min khi M là chân đường cao từ A xuống BC