Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Các phép biến một điểm A thành chính nó:
Phép đồng nhất:
- Phép tịnh tiến theo vectơ 0 .
- Phép quay tâm A, góc φ = 0º.
- Phép đối xứng tâm A.
- Phép vị tự tâm A, tỉ số k = 1.
- Ngoài ra còn có:
- Phép đối xứng trục mà trục đi qua A.
b. Các phép biến hình biến điểm A thành điểm B:
- Phép tịnh tiến theo vectơ AB .
- Phép đối xứng qua đường trung trực của đoạn thẳng AB.
- Phép đối xứng tâm qua trung điểm của AB.
- Phép quay mà tâm nằm trên đường trung trực của AB.
- Phép vị tự mà tâm là điểm chia trong hoặc chia ngoài đoạn thẳng AB theo tỉ số k.
c. Phép tịnh tiến theo vectơ v //d.
- Phép đối xứng trục là đường thẳng d’ ⊥ d.
- Phép đối xứng tâm là điểm A ∈ d.
- Phép quay tâm là điểm A ∈ d, góc quay φ =180º.
- Phép vị tự tâm là điểm I ∈ d.

a)
Các phép biến hình lần lượt là: Phép tịnh tiến theo véc tơ \(\overrightarrow{0}\); Phép quay tâm A góc \(\phi\) bất kì; phép vị tự tâm A tỉ số k bất kì.
b)
Phép tịnh tiến theo véc tơ \(\overrightarrow{AB}\); Phép đối xứng tâm qua trung điểm của AB; Phép quay tâm I là trung điểm của AB và góc \(\phi=90^o\); Phép vị tự tâm A tỉ số \(k=AB\).
c)
Phép tịnh tiến theo một véc tơ bất kì; Phép đối xứng tâm có tâm đối xứng nằm trên đường thẳng d; Phép quay bất kì; Phép vị tự có tâm nằm trên đường thẳng d.
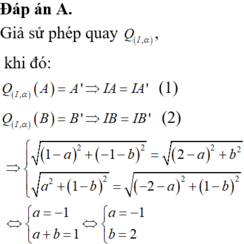

Phép quay tâm I(x;y) biến A thành A' và B thành B'nên ta có:
\(\left\{{}\begin{matrix}IA=IA'\\IB=IB'\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)^2+\left(y-3\right)^2=\left(x-1\right)^2+\left(y-5\right)^2\\\left(x-5\right)^2+\left(y+3\right)^2=\left(x-7\right)^2+\left(y+2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2+4x-6y+13=x^2+y^2-2x-10y+26\\x^2+y^2-10x+6y+34=x^2+y^2-14x+4y+53\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6x+4y-13=0\\4x+2y-19=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{25}{2}\\y=-\frac{31}{2}\end{matrix}\right.\Rightarrow x+y=-3\)