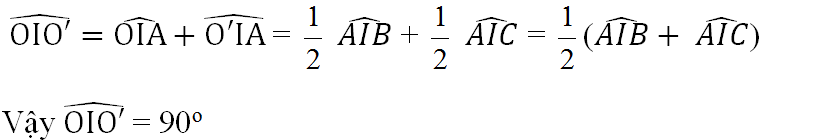Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1 2 1 2 3 4 B I C O A O'
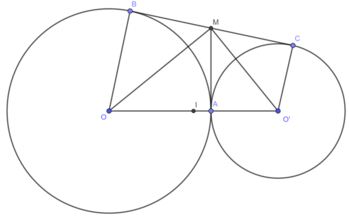
a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC .
Tam giác ABC có đường trung tuyến \(AI=\frac{1}{2}BC\)nên là tam giác vuông
Vậy \(\widehat{BAC}=90^o\left(đpcm\right)\)
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên :
\(\widehat{OIO'}=\widehat{OIA}+\widehat{O'IA}=\frac{1}{2}\widehat{AIB}+\frac{1}{2}\widehat{AIC}=\frac{1}{2}\left(\widehat{AIB}+\widehat{AIC}\right)\)
Vậy : \(\widehat{OIO'}=90^o\)
c) \(\Delta OIO'\) vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9 . 4 = 36
=> IA = 6 ( cm )
Vậy BC = 2 . IA = 2 . 6 = 12 (cm)

ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)

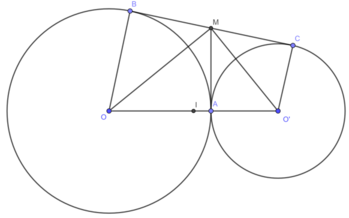
Ta có:
BM = MA
CM = MA
( tính chất hai tiếp tuyến cắt nhau)
⇒ BC = BM + MC = 2MA
Xét tam giác OMO’ vuông tại M có MA là đường cao.
Áp dụng hệ thức lượng trong tam giác vuông OMO’ có:
A M 2 = OM.O'M = 16.9 = 144 ⇒ AM = 12cm
⇒ BC = 2.12 = 24cm

c) Xét tam giác OIO' vuông tại I, IA là đường cao có:
IA 2 = O'A.OA = 4.9 = 36 ⇒ IA = 6 cm
Lại có: BC = 2 AI ⇒ BC = 12 (cm)

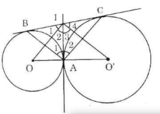
a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
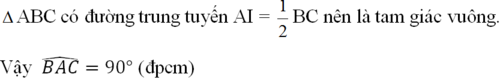
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
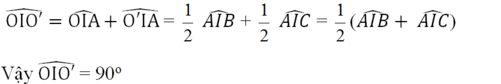
c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)

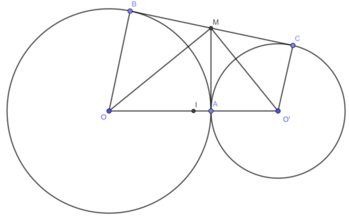
Ta có:
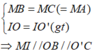
Mà OB ⊥ BC ⇒ IM ⊥ BC
Ta có:
IM ⊥ BC
BC ⋂ (I; IM) = {M}
Suy ra, BC là tiếp tuyến của đường tròn tâm I, bán kính IM

K CHO MK VỚI Ạ
HÌNH TỰ VẼ,PHẦN 1 TỰ LÀM
2, Theo tính chất hai tiếp tuyến cắt nhau ta có:
\(IA=IB=IC\)
ΔABC có đường trung tuyến \(AI=\frac{1}{2}BC\)
NÊN: ΔABC VUÔNG TẠI A
⇒ˆBAC=90 độ(dpcm)
3,Theo tính chất hai tiếp tuyến cắt nhau ta có:
\(IO=IO'\)là các tia phân giác của hai góc kề bù \(AIB,AIC\)NÊN:
4,ΔOIO' vuông tại A có:
IA là đường cao nên theo hệ thức giữa cạnh và đường cao:
\(IA^2=OA.OA'\)
\(=9.4=36\)
=>\(IA=6\)
Vậy \(BC=2.IA=2.6=12\left(cm\right)\)