Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
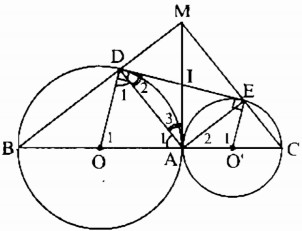
a) Kẻ tiếp tuyến chung tại A cắt DE tại I
Trong đường tròn (O) ta có:
IA = ID (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có:
Quảng cáo
IA = IE (tính chất hai tiếp tuyến cắt nhau)
Suy ra: IA=ID=IE=12DEIA=ID=IE=12DE
Tam giác ADE có đường trung tuyến AI ứng với cạnh DE và bằng nửa cạnh DE nên tam giác ADE vuông tại A.
Suy ra: ˆEAD=90∘EAD^=90∘
b) Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên ˆADB=90∘ADB^=90∘ hay ˆAEM=90∘AEM^=90∘
Mặt khác: ˆEAD=90∘EAD^=90∘ (chứng minh trên)
Tứ giác ADME có ba góc vuông nên nó là hình chữ nhật.
c) Tứ giác ADME là hình chữ nhật và ID = IE (chứng minh trên) nên đường chéo
AM của hình chữ nhật phải đi qua trung điểm I của DE. Suy ra: A, I, M thẳng hàng.
Ta có: IA ⊥ OO’ ( vì IA là tiếp tuyến của (O))
Suy ra: AM ⊥ OO’
Vậy MA là tiếp tuyến chung của đường tròn (O) và (O’).