Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

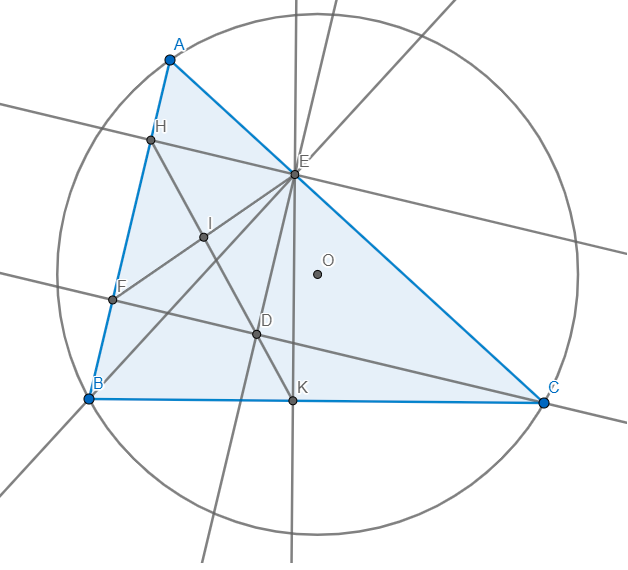
a) tam giác AEB vuông tại E có EH là đường cao \(\Rightarrow BH.BA=BE^2\)
tam giác CEB vuông tại E có EK là đường cao \(\Rightarrow BK.BC=BE^2\)
\(\Rightarrow BH.BA=BK.BC\)
b) \(BH.BA=BK.BC\Rightarrow\dfrac{BH}{BC}=\dfrac{BK}{BA}\)
Xét \(\Delta BHK\) và \(\Delta BCA:\) Ta có: \(\left\{{}\begin{matrix}\angle ABCchung\\\dfrac{BH}{BC}=\dfrac{BK}{BA}\end{matrix}\right.\)
\(\Rightarrow\Delta BHK\sim\Delta BCA\left(c-g-c\right)\)
b) \(\Delta BHK\sim\Delta BCA\Rightarrow\angle BHK=\angle BCA\)
Kẻ \(ED\bot CF\)
Vì \(\angle EHF=\angle EDF=\angle HFD=90\Rightarrow EHFD\) là hình chữ nhật
\(\Rightarrow HD\) và EF cắt nhau tại trung điểm I của mỗi đường
Vì \(\Delta EHF\) vuông tại H có I là trung điểm EF
\(\Rightarrow\angle FHI=\angle HFI=\angle AFE\left(1\right)\)
Xét \(\Delta AFC\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle AFC=\angle AEB=90\end{matrix}\right.\)
\(\Rightarrow\Delta AFC\sim\Delta AEB\left(g-g\right)\Rightarrow\dfrac{AF}{AE}=\dfrac{AC}{AB}\Rightarrow\dfrac{AF}{AC}=\dfrac{AE}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ABC:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\dfrac{AF}{AC}=\dfrac{AE}{AB}\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c-g-c\right)\Rightarrow\angle AFE=\angle ACB\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\angle FHI=\angle ACB=\angle BHK\Rightarrow\angle BHD=BHK\)
\(\Rightarrow H,D,K\) thẳng hàng \(\Rightarrow H,I,K\) thẳng hàng
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔBEA vuông tại E có EH là đường cao ứng với cạnh huyền AB, ta được:
\(BH\cdot BA=BE^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBEC vuông tại E có EK là đường cao ứng với cạnh huyền AC, ta được:
\(BK\cdot BC=BE^2\)(2)
Từ (1) và (2) suy ra \(BH\cdot BA=BK\cdot BC\)
b) Xét ΔBHK và ΔBCA có
\(\dfrac{BH}{BC}=\dfrac{BK}{BA}\)(cmt)
\(\widehat{HBK}\) chung
Do đó: ΔBHK\(\sim\)ΔBCA(c-g-c)

a,ta có góc MAB=90°; MNB=90°(gt);(góc nội tiếp chắn 1/2đtròn)
xét tứ giác AMNB có góc MAN+MNB=90°+90°=180°
suy ra AMNB nội tiếp
b, ta có góc CAB=90°(gt); CPB=90°( góc nội tiếp chắn 1/2đtròn)
xét tứ giác CPAB có góc CAB=CPB=90°
suy ra CPAB nội tiếp ( hai góc bằng nhau cùng chắn cung CB)
suy ra góc BCA=BPA(1)
góc PBA=PCA(2)
mà góc MPN=ACB=1/2sđcung MN(3)
góc PCA=PNM=1/2sđcung PM(4)
từ 1,3 suy ra góc ACB=MPN
từ 2,4 suy ra góc PNM=PBA
xét hai tam giác PAB và PMN có
góc APB=MPN(cmt)
góc PNM=PBA(cmt)
suy ra hai tam giác đó đồng dạng (đpcm)
c, ta có góc PDN=PCN=1/2sđ cung PN(1)
góc PAC=PBC(CPAB nội tiếp)(2)
mà góc PBC+PCB=90°(3)
từ 1,2,3 suy ra góc DAC+ADE=90°
suy ra DN vuông với AC
xét hai tam giác PCM và ECG có góc C chung
góc CEG=CPM=90°
suy ra hai tam giác đó đồng dạng
suy ra PC/EC=CM/CG
suy ra PC.CG=EC.CM(đpcm)

Bài 1:
A B C H F D E K L
+) Chứng minh tứ giác BFLK nội tiếp:
Ta thấy FAH và LAH là hai tam giác vuông có chung cạnh huyền AH nên AFHL là tứ giác nội tiếp. Vậy thì \(\widehat{ALF}=\widehat{AHF}\) (Hai góc nội tiếp cùng chắn cung AF)
Lại có \(\widehat{AHF}=\widehat{FBK}\) (Cùng phụ với góc \(\widehat{FAH}\) )
Vậy nên \(\widehat{ALF}=\widehat{FBK}\), suy ra tứ giác BFLK nội tiếp (Góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện)
+) Chứng minh tứ giác CELK nội tiếp:
Hoàn toàn tương tự : Tứ giác AELH nội tiếp nên \(\widehat{ALE}=\widehat{AHE}\) , mà \(\widehat{AHE}=\widehat{ACD}\Rightarrow\widehat{ALE}=\widehat{ACD}\)
Suy ra tứ giác CELK nội tiếp.

CM dễ vãi, AB, AC cắt nhau. Đường kính cất đường tròn tại giao D vs E

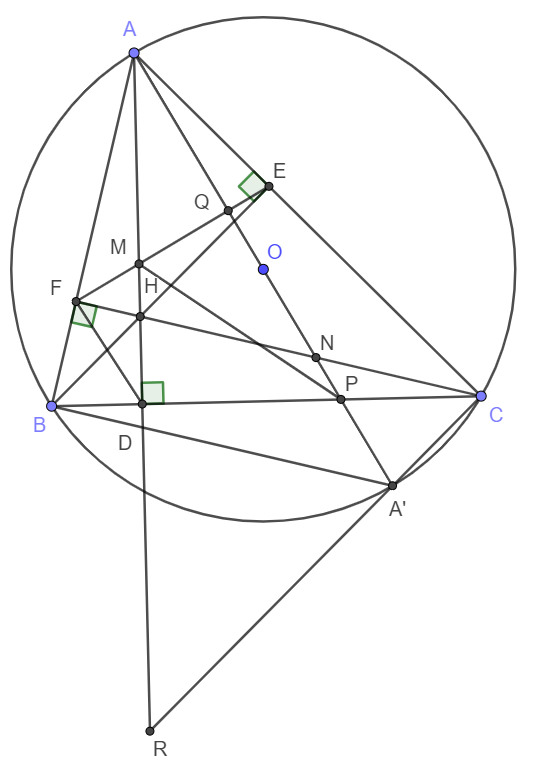
a) theo gt, BFC=BEC=90
=> BFEC nội tiếp (có 2 góc kề bang nhau)
góc AFC=ADC=90 => AFDC nội tiếp ( có 2 cạnh kề cùng nhìn một đoan thẳng bằng nhau)
b) vì tứ giác ABA'C nội tiếp => ABC = AA'C (cùng chắn cung AC)
Lại có ABC= AHF (Cùng phụ với góc BAD)
Ta thấy AFHE nội tiếp vì AFH +AEH = 90+90=180
=> AHF=AEF (Cùng chắn cung AF)
=>Đpcm
c) vì tứ giác EQA'C nôi tiếp
nên EQA'+ECA'=180 mà ECA'=90 vì là góc nội tiếp chắn nửa đường tròn
=> MQP=EQA'=90 ( vì MQP+EQA=180)
Trong đó ADC=90 =>Đpcm
d) Vì ABA'C VÀ FBDH nội tiếp nên góc NA'C=ABC=DHC
=>NA'C=DHC=>Đpcm
Câu 8:
a) Ta có:
- Góc BFC và góc BEC cùng nhìn cạnh BC dưới hai góc vuông (do BF và BE là đường cao), suy ra tứ giác BFEC nội tiếp.
Tứ giác CDHE nội tiếp vì:
- Góc CHD và góc CED cùng nhìn cạnh CD dưới hai góc vuông (do CF và DE là đường cao), suy ra tứ giác CDHE nội tiếp.
b) Theo định lý Pascal, ta có:
- Giao điểm của AH và BE là H.
- Giao điểm của HG và EK là I (do HI//DE và DE cắt EK tại I).
- Giao điểm của GB và KA là J (do HJ//DF và DF cắt KA tại J).
Vì H, I, J thẳng hàng, theo định lý Pascal, điểm K cũng phải nằm trên đường thẳng này, suy ra I, J, K thẳng hàng.
c) Ta có:
- CF là tiếp tuyến của (O) tại C (do CF là đường cao và F là tiếp điểm).
- CL là dây cung (do L nằm trên (O)).
Vì góc CFL là góc tạo bởi tiếp tuyến CF và dây cung CL, nên góc CFL bằng góc LCO (góc nội tiếp cùng chắn cung CL). Tương tự, góc LFC bằng góc LCO. Do đó, C, F, L thẳng hàng.
Ta có:
- Góc ANG bằng góc AGH (do HI//DE và HJ//DF).
- Góc AGH bằng nửa góc AOH (góc ở tâm cùng chắn cung AH).
Vì AH là đường kính của (O), nên góc AOH là góc vuông. Do đó, góc AGH là \(\dfrac{1}{2}\) góc vuông, suy ra tam giác AHG vuông tại H. Áp dụng định lý Pythagoras cho tam giác AHG, ta có:
\(AN\cdot AG=AH^2\)