Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2 phút = 120 giây, 2,5 phút = 150 giây
Vận tốc của người đi xe đạp khi lên dốc la
\(V=\dfrac{s}{t}=120:120=1\left(ms\right)\)
Vận tốc của người đi xe đạp xuống dốc là
\(V=\dfrac{s}{t}=420:150=2,8\left(ms\right)\)
Vận tốc trung bình của người đó trên cả 2 quãng đường là
\(V_{tb}=\dfrac{S+S_1}{t+t_1}=\dfrac{120+420}{120+150}=\dfrac{540}{270}=2\left(ms\right)\)
Đổi 2m/s =7,2 km/h

mÌNH MỎI TAY QUÁ
Lấy gốc tọa độ tại AA chiều dương là chiều từ AA đến BB. Gốc thời gian là lúc 7h7h
Phương trình chuyển động của :
Xe đi từ A:A: xA=36t(km−h)xA=36t(km−h)
Xe đi từ B:xB=96−28t(km−h)B:xB=96−28t(km−h)
Hai xe gặp nhau khi :xA=xB:xA=xB
→36t=96−28t→36t=96−28t
⇒t=1,5(h)⇒t=1,5(h)
xA=36t=36.1,5=54(km)xA=36t=36.1,5=54(km)
Hai xe gặp nhau lúc 8h30′8h30′. Nơi gặp nhau cách AA 54km54km
TH1:TH1: Hai xe cách nhau 24km24km trước khi hai xe gặp nhau
Hai xe cách nhau 24km
⇔⇔ xB−xA=24xB−xA=24
⇔⇔ 96−28t′−36t′=2496−28t′−36t′=24
⇔t′=1,125h⇔t′=1,125h
Vậy lúc 8h7phút30giây hai xe cách nhau 24km
TH2:TH2: Hai xe cách nhau 24k sau khi gặp nhau
Hai xe cách nhau 24km
⇔xA−xB=24⇔xA−xB=24
⇔36t′′−96+28t′′=24⇔36t″−96+28t″=24
⇔t′′=1,875(h)⇔t″=1,875(h)
Vậy lúc 8h52phút30giây hai xe cách nhau 24km
bài 2:
ta có:
thời gian người đó đi trên nửa quãng đường đầu là:
t1=S1/v1=S/2v1=S/24
thời gian người đó đi hết nửa đoạn quãng đường cuối là:
t2=S2/v2=S2/v2=S/40
vận tốc trung bình của người đó là:
vtb=S/t1+t2=S/(S/40+S/24)=S/S(140+124)=1/(1/24+1/40)
⇒vtb=15⇒vtb=15 km/h
bài 3:
thời gian đi nửa quãng đầu t1=(1/2) S.1/25=S/50
nửa quãng sau (1/2) t2.18+(1/2) t2.12=(1/2) S⇔t2=S/30
vận tốc trung bình vtb=S/(t1+t2)=S/S.(1/50+1/30)=1/(1/50+1/30)=18,75(km/h)
HT

(3,0 điểm)
Tóm tắt: (0,5 điểm)
s 1 = 300m; t 1 = 2 phút = 120 s
s 2 = 500m; t 2 = 2,5 phút = 150 s
Tính: v tb = ?
Giải
Vận tốc trung bình của người đi xe đạp trên cả hai quãng đường là: (0,5 điểm)
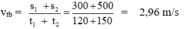 (0,5 điểm)
(0,5 điểm)

Bài 1: Tóm tắt
\(S_1=24km\)
\(V_1=12km\)/\(h\)
\(S_2=12km\)
\(V_2=45'=0,75h\)
_______________
a) \(t_1=?\)
b) \(V_{TB}\)
Giải
a) Thời gian người đó đạp xe trên quãng đường đầu là: \(t_1=\frac{S_1}{V_1}=\frac{24}{12}=2\left(h\right)\)
b) Ta có công thức tính vận tốc trung bình là: \(V=\frac{S_1+S_2+....+S_n}{t_1+t_2+t_3+....+t_n}\)
Vậy vận tốc trung bình của người đó trên quãng đường là:
\(V_{TB}=\frac{S_1+S_2}{t_1+t_2}=\frac{24+12}{2+0,75}\approx13\)(km/h)
Bài 2: Tóm tắt
\(S_1=600m=0,6km\)
\(t_1=2'=\frac{1}{30}\left(h\right)\)
\(S_2=10,8km\)
\(t_2=0,75h\)
_________________
a) \(V_1=?;V_2=?\)
b) \(S_{KC}=?\)
Giải
a) Vận tốc của người thứ nhất là: \(V_1=\frac{S_1}{t_1}=\frac{0,6}{\frac{1}{30}}=18\)(km/h)
Vận tốc của người thứ 2 là: \(V_2=\frac{S_2}{t_2}=\frac{10,8}{0,75}=14,4\) (km/h)
=> Người thứ nhất đi nhanh hơn người thứ 2.
b) Do đi cùng lúc => thời gian đi của 2 người là như nhau và vận tốc đã cho
=> Hai người cách nhau số km là: \(S-t\left(V_1+V_2\right)=S-\frac{1}{3}\left(18+14,4\right)=S-10,8\)
Theo đề thì còn cần phải dựa vào khoảng cách của 2 người khi 2 người bắt đầu đi nữa.
a) Thời gian người đó đạp xe trên quãng đường thứ nhất là :
24 : 12 = 2 (giờ)
b) Đổi : 45 phút = 0,75 giờ
=> Vận tốc trung bình của người đi xe đạp trên cả quãng đường là :
(S1 + S2) / (t1 + t2) = (12+24) / (2+0,75) = 13 (km/h)

1)
s1 = 100m
t1 = 25s
s2 = 50m
t2 = 20s
Vận tốc trong bình của xe trên quãng đường xuống dốc là:
vtb1 = \(\frac{s_1}{t_1}=\frac{100}{25}=4\)(m/s)
Vận tốc trung bính của xe trên quãng đường xe lăn tiếp là:
vtb2 = \(\frac{s_2}{t_2}=\frac{50}{20}=2,5\)(m/s)
Vận tốc trung bình của xe trên cả đoạn đường là:
vtb = \(\frac{s_1+s_2}{t_1+t_2}=\frac{100+50}{25+20}=3,\left(3\right)\)(m/s)
2) Gọi s là quãng đường AB
t1 là thời gian đi trên nửa quãng đường đầu
t2 là thời gian đi trên nửa quãng đường sau
s1 là nửa quãng đường đầu.
s2 là nửa quãng đường sau
s1 = s2 = \(\frac{s}{2}\)
Thời gian xe chạy trên nửa quãng đường đầu là:
t1 = \(\frac{s_1}{v_1}=\frac{s}{2.5}=\frac{s}{10}\)(s)
Thời gian xe chạy trên nửa quãng đường sau là:
t2 = \(\frac{s_2}{v_2}=\frac{s}{2.3}=\frac{s}{6}\)(s)
Vận tốc trung bình trên cả đoạn đường AB là :
\(v_{tb}=\frac{s_1+s_2}{t_1+t_2}=\frac{s}{\frac{s}{10}+\frac{s}{6}}=\frac{1}{\frac{1}{10}+\frac{1}{6}}=3,75\)(m/s)

Câu 1:
Vận tốc quãng đường xuống dốc:
\(v_1=\dfrac{S_1}{t_1}=\dfrac{150}{30}=5\left(m/s\right)\)
Vận tốc quãng đường thứ 2:
\(v_2=\dfrac{S_2}{t_2}=\dfrac{90}{15}=6\left(m/s\right)\)
Vận tốc tb cả 2 quãng đường:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{150+90}{30+15}=\dfrac{16}{3}\left(m/s\right)\)
Câu 2:
Đổi: \(4m/s=14,4km/h\)
Thời gian đi bộ trên đoạn đường đầu:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{8}{14,4}=\dfrac{5}{9}\left(h\right)\)
Vận tốc tb trên cả 2 đoạn đường:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{8+4,8}{\dfrac{5}{9}+2,5}\approx4,2\left(km/h\right)\)

Gọi S(km) là quãng đường AB(S>0)
\(10\left(\dfrac{m}{s}\right)=36\left(\dfrac{km}{h}\right)\)
\(\left\{{}\begin{matrix}t_1=\dfrac{S_1}{v_1}=\dfrac{S}{2.40}=\dfrac{S}{80}\left(h\right)\\t_2=\dfrac{S_2}{v_2}=\dfrac{S}{2.36}=\dfrac{S}{72}\left(h\right)\end{matrix}\right.\)
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{S}{\dfrac{S}{80}+\dfrac{S}{72}}=\dfrac{S}{S.\dfrac{19}{720}}\approx38\left(\dfrac{km}{h}\right)\)

Đổi 9 km/h=2,5 m/s
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{s_1+s_2}{t_1+\dfrac{s_2}{v_2}}=\dfrac{120+60}{30+\dfrac{60}{2,5}}=\dfrac{10}{3}\left(\dfrac{m}{s}\right)\)
Câu 38:
\(v_{tb}=\dfrac{s'+s''}{t'+t''}=\dfrac{2,5+1,5}{\left(2,5:5\right)+\dfrac{24}{60}}=4,\left(4\right)\left(km/h\right)\)
Câu 37:
\(24\left(\dfrac{m}{s}\right)=86,4\left(\dfrac{km}{h}\right);36000\left(\dfrac{m}{min}\right)=2160\left(\dfrac{km}{h}\right)\)
\(\Rightarrow52\left(\dfrac{km}{h}\right)< 86,4\left(\dfrac{km}{h}\right)< 2160\left(\dfrac{km}{h}\right)\)
\(\Rightarrow52\left(\dfrac{km}{h}\right)< 24\left(\dfrac{m}{s}\right)< 36000\left(\dfrac{m}{min}\right)\)
Câu 35:
\(v_{tb}=\dfrac{s'+s''}{t'+t''}=\dfrac{120+60}{30+24}=3,\left(3\right)\left(\dfrac{m}{s}\right)\)