Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) A = 3/7
b) B = 73/13
c) C = 37/7
d) D = 12
ba câu a) ,b) ,c) bn đổi ra hỗn số giúp mk nha
tick cho tớ nha

a: \(=\dfrac{4\cdot2+4\cdot9}{55}+\dfrac{5}{6}=\dfrac{4}{5}+\dfrac{5}{6}=\dfrac{49}{30}\)
b: \(=\dfrac{3}{2}\cdot\dfrac{3}{5}-\left(\dfrac{3}{7}+\dfrac{3}{20}\right)\cdot\dfrac{10}{3}\)
\(=\dfrac{9}{10}-\dfrac{81}{140}\cdot\dfrac{10}{3}\)
\(=\dfrac{9}{10}-\dfrac{27}{14}=\dfrac{-36}{35}\)
c: \(=15+\dfrac{3}{13}-3-\dfrac{4}{7}-8-\dfrac{3}{13}\)
\(=4-\dfrac{4}{7}=\dfrac{24}{7}\)
d: \(=\dfrac{-7}{9}\left(\dfrac{4}{11}+\dfrac{7}{11}\right)+5+\dfrac{7}{9}=5\)

b: \(A=5\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{26\cdot31}\right)\)
\(=5\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{26}-\dfrac{1}{31}\right)\)
\(=5\cdot\dfrac{30}{31}=\dfrac{150}{31}\)
c: \(C=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}\)
=1-1/16=15/16

a, \(A-B=\frac{3}{8^3}+\frac{7}{8^4}-\frac{7}{8^3}-\frac{3}{8^4}==\left(\frac{7}{8^4}-\frac{3}{8^4}\right)-\left(\frac{7}{8^3}-\frac{3}{8^3}\right)=\frac{4}{8^4}-\frac{4}{8^3}< 0\)
Vậy A < B
b, \(A=\frac{10^7+5}{10^7-8}=\frac{10^7-8+13}{10^7-8}=1+\frac{13}{10^7-8}\)
\(B=\frac{10^8+6}{10^8-7}=\frac{10^8-7+13}{10^8-7}=1+\frac{13}{10^8-7}\)
Vì \(10^7-8< 10^8-7\Rightarrow\frac{1}{10^7-8}>\frac{1}{10^8-7}\Rightarrow\frac{13}{10^7-8}>\frac{13}{10^8-7}\Rightarrow A>B\)
c,Áp dụng nếu \(\frac{a}{b}>1\Rightarrow\frac{a}{b}>\frac{a+n}{a+n}\) có:
\(B=\frac{10^{1993}+1}{10^{1992}+1}>\frac{10^{1993}+1+9}{10^{1992}+1+9}=\frac{10^{1993}+10}{10^{1992}+10}=\frac{10\left(10^{1992}+1\right)}{10\left(10^{1991}+1\right)}=\frac{10^{1992}+1}{10^{1991}+1}=A\)
Vậy A < B

\(A=11\dfrac{3}{13}-\left(2\dfrac{4}{7}+5\dfrac{3}{13}\right)\)
\(A=11\dfrac{3}{13}-5\dfrac{3}{13}-2\dfrac{4}{7}\)
\(A=6-2\dfrac{4}{7}\)
\(A=5\dfrac{7}{7}-2\dfrac{4}{7}\)
\(A=3\dfrac{3}{7}\)
\(B=\left(6\dfrac{4}{9}+3\dfrac{7}{11}\right)-4\dfrac{4}{9}\)
\(B=\left(6\dfrac{4}{9}-4\dfrac{4}{9}\right)+3\dfrac{7}{11}\)
\(B=2+3\dfrac{7}{11}\)
\(B=5\dfrac{7}{11}\)
\(C=\dfrac{-5}{7}.\dfrac{2}{11}+\dfrac{-5}{7}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\left(\dfrac{2}{11}+1\right)-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\dfrac{13}{11}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-65}{77}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{4}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{160}{11}\)
\(D=0,7.2\dfrac{2}{3}.20.0,375.\dfrac{5}{28}\)
\(D=\dfrac{7}{10}.\dfrac{8}{3}.20.\dfrac{375}{1000}.\dfrac{5}{28}\)
\(D=\dfrac{7}{28}=\dfrac{5}{2}\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-0,25-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{12}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right).0\)
\(\Rightarrow E=0\)

B= (7 \(\dfrac{4}{9}\) + 3\(\dfrac{8}{13}\)) - 5\(\dfrac{4}{9}\)
B=(\(\dfrac{67}{9}\)+ \(\dfrac{47}{13}\)) - \(\dfrac{49}{9}\)
B=\(\dfrac{116}{9}\)-\(\dfrac{47}{13}\)
B=\(\dfrac{116-47}{117}\)
B=\(\dfrac{23}{39}\)
tui cũng không biết đúng hông nữa ![]()
Đề bài : Áp dụng tính chất các phép tính và quy tắc dấu ngoặc để tính giá trị các biểu thức

A = \(\dfrac{1}{4}.\dfrac{7}{3}.12\)
= \(\dfrac{1.7.12}{4.3}\)
= \(7\)
@Nguyễn Thành Đăng
B = \(\dfrac{3}{8}.56.\dfrac{25}{7}.\left(-4\right)\)
= \(-\dfrac{3.56.25.4}{8.7}\)
= -3.100
= -300
@Nguyễn Thành Đăng

CÁCH 1 : A = \(\dfrac{235}{11}-\left(\dfrac{8}{5}+\dfrac{81}{11}\right)\)
A = \(\dfrac{235}{11}-\left(\dfrac{88}{55}+\dfrac{405}{55}\right)\)
A = \(\dfrac{235}{11}-\dfrac{493}{55}\)
A = \(\dfrac{1175}{55}+\dfrac{493}{55}\)
A = \(\dfrac{1668}{55}\)
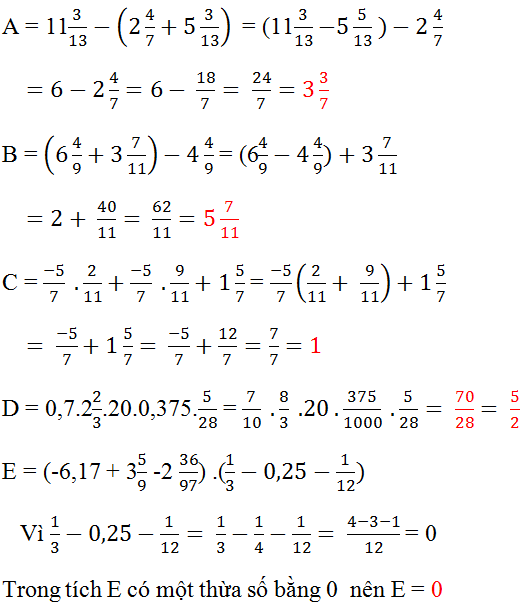
C
sai r D moi dung