Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Phương pháp
Sử dụng công thức C n k = n ! k ! n − k ! tìm n.
Sử dụng khai triển nhị thức Newton
a + b n = ∑ k = 0 n C n k . a n − k . b k
Cách giải
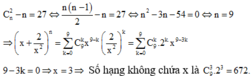

Từ phương trình C n 3 + 2 n = A n + 1 2 nên n = 8
Với n = 8, ta có
2 x - 3 x 3 2 n = 2 x - 3 x 3 16 = ∑ k = 0 16 . C 16 k . 2 x 16 - k - 3 x 3 = ∑ k = 0 16 . C 16 k . 2 x 16 - k . - 3 k . x 16 - 4 k 3
Số hạng không chứa x ứng với 16 - 4 k 3 = 0 ⇔ k = 12
số hạng cần tìm C 16 12 . 2 4 . 3 12
Chọn C

Đáp án C
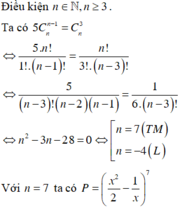
Số hạng thứ k + 1 trong khai triển T k + 1 = − 1 k 2 7 − k . C 7 k . x 14 − 3 k
Suy ra 14 − 3 k = 5 ⇔ k = 3
Vậy số hạng chứa x 5 trong khai triển là T 4 = − 35 16 x 5 .




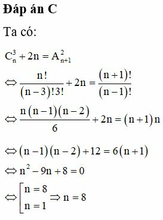


Chọn đáp án A
Lưu ý: Ta có thể xác định n bằng MTCT CASIO fx–580 VN X như sau: