
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

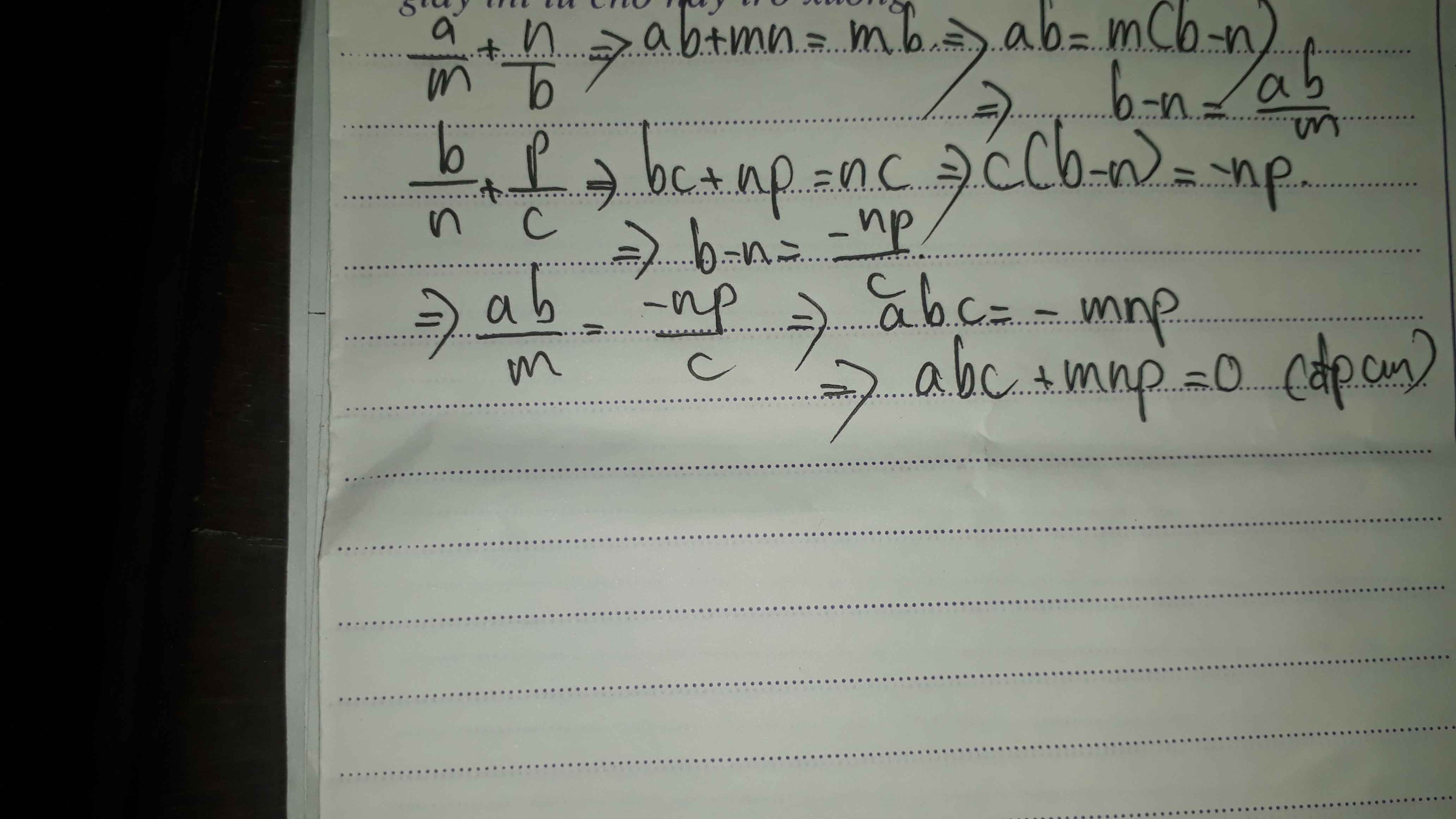


\(\dfrac{a}{a'}+\dfrac{b'}{b}=1\Rightarrow\dfrac{a}{a'}\cdot\dfrac{b}{b'}+\dfrac{b'}{b}\cdot\dfrac{b}{b'}=\dfrac{b}{b'}\Rightarrow\dfrac{ab}{a'b'}+1=\dfrac{b}{b'}\left(1\right)\)
\(\dfrac{b}{b'}+\dfrac{c'}{c}=1\Rightarrow\dfrac{b}{b'}=1-\dfrac{c'}{c}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\dfrac{ab}{a'b'}=-\dfrac{c'}{c}\Rightarrow abc=-a'b'c'\Rightarrow abc+a'b'c'=0\)
Vậy \(abc+a'b'c'=0\left(dpcm\right)\)
cho ba số a,b,c thỏa mãn a.b.c = 1 . CMR: \(\frac{1}{ab+a+1}+\frac{1}{bc+b+1}+\frac{1}{abc+bc+b}=1\)

Lời giải:
Dựa vào điều kiện $abc=1$ ta có:
\(\frac{1}{ab+a+1}+\frac{1}{bc+b+1}+\frac{1}{abc+ca+c}=\frac{1}{ab+a+1}+\frac{1}{bc+b+1}+\frac{1}{1+ca+c}\)
\(=\frac{1}{ab+a+1}+\frac{a}{abc+ab+a}+\frac{ab}{ab+ab.ca+ab.c}\)
\(=\frac{1}{ab+a+1}+\frac{a}{1+ab+a}+\frac{ab}{ab+a+1}=\frac{1+a+ab}{ab+a+1}=1\)
Ta có đpcm.
Ta có: \(a.b.c=1\)
\(=\frac{1}{ab+a+1}+\frac{1}{bc+b+1}+\frac{1}{abc+bc+b}\)
\(=\frac{1}{ab+a+1}+\frac{ab}{abc+ab+a}+\frac{a}{abc.a+abc+ab}\)
\(=\frac{1}{ab+a+1}+\frac{ab}{1+ab+a}+\frac{a}{a+1+ab}\)
\(=\frac{1+ab+a}{1+ab+a}\)
\(=1.\)
\(\Rightarrow\frac{1}{ab+a+1}+\frac{1}{bc+b+1}+\frac{1}{abc+bc+b}=1\left(đpcm\right).\)
Chúc bạn học tốt!
cho ba số a,b,c thỏa mãn a.b.c = 1 . CMR: \(\frac{1}{ab+a+1}+\frac{1}{bc+b+1}+\frac{1}{abc+bc+b}=1\)


Ta có :
\(A=\dfrac{a}{ab+a+1}+\dfrac{b}{bc+b+1}+\dfrac{c}{ac+c+1}\)
\(A=\dfrac{a}{ab+a+1}+\dfrac{ab}{abc+ab+a}+\dfrac{abc}{aabc+abc+ab}\)
\(A=\dfrac{a}{ab+a+1}+\dfrac{ab}{1+ab+a}+\dfrac{1}{a+1+ab}\)
\(A=\dfrac{a+ab+1}{ab+a+1}\)
\(\Rightarrow A=1\left(đpcm\right)\)
