Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔKNM vuông tại K và ΔMNP vuông tại M có
\(\widehat{N}\) chung
Do đó: ΔKNM~ΔMNP
Xét ΔMNP vuông tại M và ΔKMP vuông tại K có
\(\widehat{P}\) chung
Do đó: ΔMNP~ΔKMP
=>ΔKNM~ΔMNP~ΔKMP
b: Ta có: ΔKNM~ΔKMP
=>\(\dfrac{KN}{KM}=\dfrac{KM}{KP}\)
=>\(KM^2=KN\cdot KP\)
c: ta có: NP=NK+KP
=4+9
=13(cm)
Ta có: \(KM^2=KN\cdot KP\)
=>\(KM^2=4\cdot9=36\)
=>\(KM=\sqrt{36}=6\left(cm\right)\)
Xét ΔMNP vuông tại M có MK là đường cao
nên \(S_{MNP}=\dfrac{1}{2}\cdot MK\cdot PN=\dfrac{1}{2}\cdot6\cdot13=39\left(cm^2\right)\)

a: Xét ΔKNM vuông tại K và ΔMNP vuông tại M có
góc N chung
=>ΔKNM đồng dạng với ΔMNP
Xét ΔKMP vuông tại K và ΔMNP vuông tại M có
góc P chung
=>ΔKMP đồng dạng với ΔMNP
b: ΔKNM đồng dạng với ΔKMP
=>KN/KM=KM/KP
=>KM^2=KN*KP
c: \(MK=\sqrt{4\cdot9}=6\left(cm\right)\)
\(S_{MNP}=\dfrac{1}{2}\cdot6\cdot13=3\cdot13=39\left(cm^2\right)\)

a) Ta có: \(\Delta ABC \backsim \Delta MNP\) suy ra \(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\,\,\left( 1 \right)\) và \(\widehat B = \widehat N\)
Mà D là trung điểm BC và Q là trung điểm NP nên \(BC = 2BD\) và \(NP = 2NQ\)
Thay vào biểu thức (1) ta được \(\frac{{AB}}{{MN}} = \frac{{2BD}}{{2NQ}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\)
Xét tam giác ABD và tam giác MNQ có:
\(\frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\) và \(\widehat B = \widehat N\)
\( \Rightarrow \Delta ABD \backsim \Delta MNQ\) (c-g-c)
b) Vì \(\Delta ABD \backsim \Delta MNQ\) nên ta có \(\frac{{AB}}{{MN}} = \frac{{AD}}{{MQ}}\,\,\left( 2 \right)\) và \(\widehat {BAD} = \widehat {NMQ}\) hay \(\widehat {BAG} = \widehat {NMK}\)
Mà G và K lần lượt là trọng tâm của tam giác ABC và tam giác MNP nên \(AD = \frac{3}{2}AG\) và \(MQ = \frac{3}{2}MK\).
Thay vào (2) ta được: \(\frac{{AB}}{{MN}} = \frac{{\frac{3}{2}AG}}{{\frac{3}{2}MK}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\)
Xét tam giác ABG và tam giác NMK có:
\(\frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\) và \(\widehat {BAG} = \widehat {NMK}\)
\( \Rightarrow \)\(\Delta ABG \backsim \Delta MNK\) (c-g-c)

a) Vì tam giác \(\Delta MNP\backsim\Delta ABC\) nên \(\widehat B = \widehat N\) (hai góc tương ứng).
Vì \(MK\) là đường cao nên \(\widehat {MKN} = 90^\circ \);Vì \(AH\) là đường cao nên \(\widehat {AHB} = 90^\circ \)
Xét \(\Delta MNK\) và \(\Delta ABH\) có:
\(\widehat B = \widehat N\) (chứng minh trên)
\(\widehat {MKN} = \widehat {AHB} = 90^\circ \)
Do đó, \(\Delta MNK\backsim\Delta ABH\) (g.g)
Vì \(\Delta MNK\backsim\Delta ABH\) nên ta có: \(\frac{{MN}}{{AB}} = \frac{{NK}}{{BH}} = \frac{{MK}}{{AH}} = k \Rightarrow \frac{{MK}}{{AH}} = k\).
b) Vì \(\Delta MNP\backsim\Delta ABC\) nên \(\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}} = k\)
\( \Rightarrow \frac{{NP}}{{BC}} = k \Leftrightarrow NP = kBC\)
Vì \(\frac{{MK}}{{AH}} = k \Rightarrow MK = kAH\)
Diện tích tam giác \(MNP\) là:
\({S_1} = \frac{1}{2}.MK.NP\) (đvdt)
Diện tích tam giác \(ABC\) là:
\({S_2} = \frac{1}{2}.AH.BC\) (đvdt)
Ta có: \(\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{1}{2}.MK.NP}}{{\frac{1}{2}.AH.BC}} = \frac{{kAH.kBC}}{{AH.BC}} = {k^2}\) (điều phải chứng minh)

Khẳng định d) là khẳng định không đúng
=> ΔACB \(\backsim\) ΔMPN

Đáp án đúng là A
Vì \(\Delta ABC\backsim\Delta MNP\) theo tỉ số \(k = 3\) nên \(\Delta MNP\backsim\Delta ABC\) theo tỉ số \(\frac{1}{3}\).

Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 50^\circ + 60^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 70^\circ \end{array}\)
Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P = 70^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g).
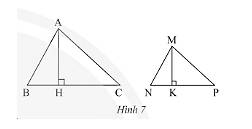
a: Xét ΔKNM vuông tại K và ΔMNP vuông tại M có
\(\widehat{N}\) chung
Do đó: ΔKNM~ΔMNP
Xét ΔKNM vuông tại K và ΔKMP vuông tại K có
\(\widehat{KNM}=\widehat{KMP}\left(=90^0-\widehat{KMN}\right)\)
Do đó; ΔKNM~ΔKMP
b: Ta có: ΔKNM~ΔKMP
=>\(\dfrac{KN}{KM}=\dfrac{KM}{KP}\)
=>\(KM^2=KN\cdot KP\)
c: Xét ΔMNP vuông tại M có MK là đường cao
nên \(MK^2=KN\cdot KP\)
=>\(MK^2=4\cdot9=36=6^2\)
=>\(MK=\sqrt{6^2}=6\left(cm\right)\)
PN=PK+NK
=4+9=13(cm)
Xét ΔMNP có MK là đường cao
nên \(S_{MNP}=\dfrac{1}{2}\cdot MK\cdot NP=\dfrac{1}{2}\cdot6\cdot13=3\cdot13=39\left(cm^2\right)\)
a: Xét ΔKNM vuông tại K và ΔMNP vuông tại M có
�^
N chung
Do đó: ΔKNM~ΔMNP
Xét ΔKNM vuông tại K và ΔKMP vuông tại K có
��^=���^(=900−���^)KNM=KMP(=90−KMN)
Do đó; ΔKNM~ΔKMP
KN/KM = KM/KP
b: Ta có ΔKNM~ΔKMP
=>��2=��⋅��KM2 = KN.KP
c: Xét ΔMNP vuông tại M có MK là đường cao
nên ��2=��⋅��MK2=KN2.KP2
MK2 = 42 + 92
MK2= 36
MK =6