K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
2
10 tháng 6 2017
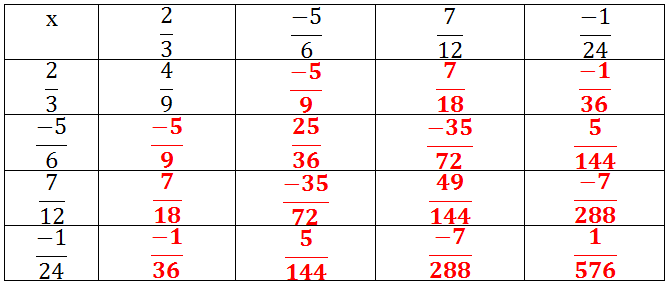
Kết quả tìm được đúng
Phương pháp này không thể áp dụng để rút gọn các phân số có dạng \(\dfrac{\overline{ab}}{\overline{bc}}\)
VD: Phân số \(\dfrac{26}{64}\) có dạng \(\dfrac{\overline{ab}}{\overline{bc}}\) nhưng khi rút gọn thì được phân số \(\dfrac{13}{32}\) , chứ không phải phân số \(\dfrac{1}{2}\) theo phương pháp trên ta có được.
Hoặc là phân số \(\dfrac{18}{88}\) có dạng \(\dfrac{\overline{ab}}{\overline{bc}}\) nhưng khi rút gọn thì được phân số \(\dfrac{9}{44}\) , chứ không phải phân số \(\dfrac{1}{8}\) theo phương pháp trên ta có được.
6 tháng 5 2018
Kiểm tra ta thấy các kết quả tìm được đều đúng. Tuy nhiên, không thể áp dụng "phương pháp" trên để rút gọn các phân số có dạng ab/bc.
Ví dụ : 
Cách "rút gọn" của bạn Minh chỉ đúng một cách ngẫu nhiên
SG
2
SG
2
17 tháng 4 2017
|
+ |
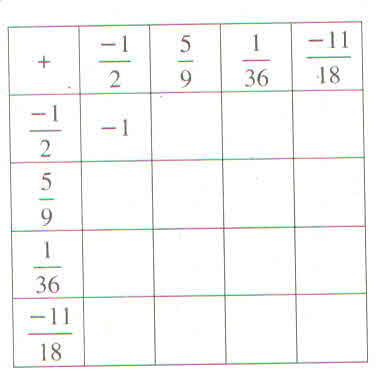
−12−12 |
5959 |
136136 |
−1118−1118 |
|
−12−12 |
- 1 |
118118 |
−1736−1736 |
−109−109 |
|
5959 |
118118 |
109109 |
712712 |
−118−118 |
|
136136 |
−1736−1736 |
712712 |
118118 |
−712−712 |
|
−1118−1118 |
−109−109 |
−118−118 |
−712−712 |
|
17 tháng 4 2017
|
+ |
−12−12 |
5959 |
136136 |
−1118−1118 |
|
−12−12 |
- 1 |
118118 |
−1736−1736 |
−109−109 |
|
5959 |
118118 |
109109 |
712712 |
−118−118 |
|
136136 |
−1736−1736 |
712712 |
118118 |
−712−712 |
|
−1118−1118 |
−109−109 |
−118−118 |
−712−712 |
−119−119 |
T
9 tháng 4 2022
Câu 14)
\(a,\\ =-\dfrac{3}{8}+\dfrac{8}{17}+\dfrac{-5}{8}-\dfrac{3}{5}+\dfrac{9}{17}\\ =\left(\dfrac{-3}{8}+\dfrac{-5}{8}\right)+\left(\dfrac{8}{17}+\dfrac{9}{17}\right)-\dfrac{3}{5}\\ =\left(-1\right)+1-\dfrac{3}{5}=0-\dfrac{3}{5}=\dfrac{-3}{5}\\ b,\\ =\dfrac{7}{15}.\dfrac{-15}{14}+\left(\dfrac{27}{16}-\dfrac{1}{8}\right):\dfrac{5}{8}\)
\(=\dfrac{-1}{2}+\dfrac{25}{16}.\dfrac{8}{5}=\dfrac{-1}{2}+\dfrac{5}{2}=2\\ c,\\ =\dfrac{2}{2}-\dfrac{2}{3}+\dfrac{2}{3}-\dfrac{2}{4}+.....+\dfrac{2}{99}-\dfrac{2}{100}\\ =1-\dfrac{1}{50}=\dfrac{49}{50}\)
Câu 15
\(a,2x+\dfrac{-1}{4}=\dfrac{3}{2}\\ 2x=\dfrac{3}{2}-\dfrac{-1}{4}=\dfrac{7}{4}\\ x=\dfrac{7}{4}:2=\dfrac{7}{8}\\ b,\dfrac{15}{x}=\dfrac{-3}{4}\\ x=\dfrac{15.4}{-3}=-20\)
18 tháng 4 2017
Giải:
|
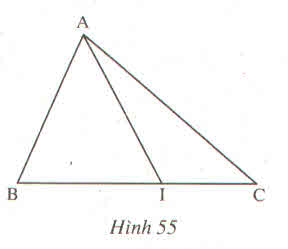
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
|
A,B,I |
|
AB, BI, IA |
|
|
A,I,C |
|
AI, IC, CA |
|
|
A,B,C |
|
AB, BC, CA |
SG
4
18 tháng 4 2017
Giải:
|
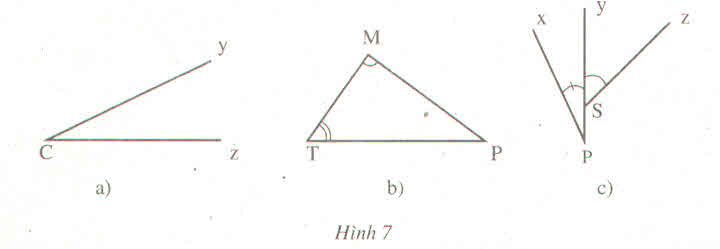
Hình |
Tên góc (cách viết thông thường) |
Tên đỉnh |
Tên cạnh |
Tên góc (Cách viết kí hiệu) |
|
a |
Góc yCz, góc zCy, góc C |
C |
Cy,Cz |
|
|
b |
Góc MTP, PTM, T Góc TMP, PMT,M Góc TPM, MPT,P |
T M P |
TM,TP MT,MP PT,PM |
|
|
c |
Góc xPy,yPx,P Góc ySz,zSy |
P S |
Px, Py Sy, Sz |
|
SG
1
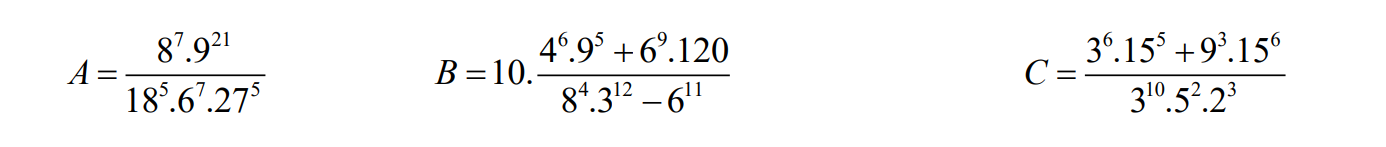
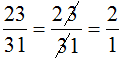
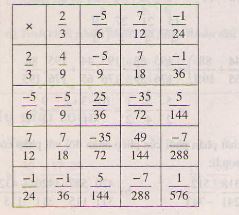
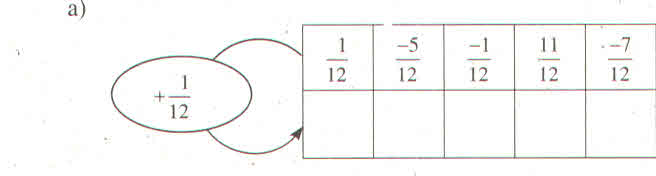
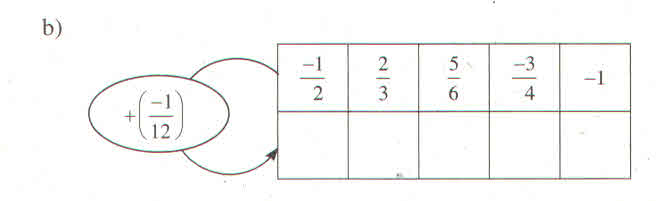
\(A=\dfrac{8^7\cdot9^{21}}{18^5\cdot6^7\cdot27^5}=\dfrac{2^{21}\cdot3^{42}}{2^{12}\cdot3^{32}}=2^9\cdot3^{10}\)
\(B=10\cdot\dfrac{4^6\cdot9^5+6^9\cdot120}{8^4\cdot3^{12}-6^{11}}=10\cdot\dfrac{2^{12}\cdot3^{10}+2^{12}\cdot3^{10}\cdot5}{2^{12}\cdot3^{12}-2^{11}\cdot3^{11}}\)
\(=10\cdot\dfrac{2^{13}\cdot3^{11}}{2^{11}\cdot3^{11}\cdot5}\)
\(=10\cdot2^2\cdot\dfrac{1}{5}=8\)