Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

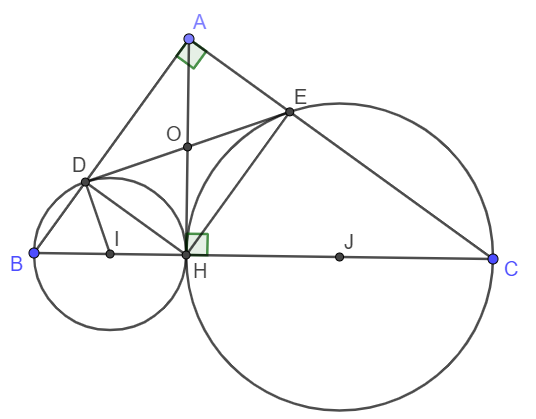
Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chỉ cần chứng minh ID\perp DEID⊥DE .
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC nên ta có: \widehat{BDH}=\widehat{CEH}=90^oBDH=CEH=90o.
Suy ra tứ giác ADHE là hình chữ nhật.
Gọi O là giao điểm của AH và DE, khi đó ta có OD = OH = OE = OA.
Suy ra tam giác ODH cân tại O vì vậy \widehat{ODH}=\widehat{OHD}ODH=OHD.
Ta cũng có tam giác IDH cân tại I suy ra \widehat{IDH}=\widehat{IHO}IDH=IHO.
Suy ra \widehat{IDO}+\widehat{OHD}=\widehat{IHD}+\widehat{IHA}=90^oIDO+OHD=IHD+IHA=90o \Leftrightarrow\widehat{IDO}=90^o⇔IDO=90o hay DI \perp⊥ DE.
Ta có DI\perp DE\left(D\in\left(I\right)\right)DI⊥DE(D∈(I)) suy ra DE tiếp xúc với (I) tại D.
Chứng minh tương tự ta cũng có DE tiếp xúc với (J) tại E.
Vậy DE là tiếp tuyến chung của đường tròn (I) và đường tròn (J).
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC nên ta có : góc BHD = góc CEH=90°
=> tứ giác ADHE là hình chữ nhật
Gọi O là giao điểm của AH và DE khi đó ta có OD=OE=OA
=> Tam giác ODH cân tại O vì vậy góc ODH = góc OHD
Ta cũng có tam giác IDH cân tại I suy ra góc IDH= góc IHO
=> góc IDO + góc OHD = góc IHD + góc IHA=90° <=> góc IDO = 90° hay DI ⊥ DE
ta có DI ⊥ DE ( D ∈ I) => DE tiếp xúc với (I) tại D
Ta có DE tiếp xúc với (J) tại E
Vậy DE là tiếp tuyến chung của đường tròn (I) và đường tròn (J)
\perp \perp⊥\perp⊥\per⊥\perp⊥

a/ Ta có góc BDC=90 độ ( góc nt chăn nửa đường tròn)
suy ra góc ADH = 90 độ ( kề bù )
góc BEC= 90 độ ( góc nt chắn nửa đường tròn)
suy ra góc AEH = 90 độ ( kề bù )
Tư giác ADHE có góc ADH + góc AEH = 90 độ + 90 độ = 180 độ
Hại góc ở vị tri đối nhau . Do đó tứ giác ADHE nt đường tròn.
b/
c/Ta có góc BDC = 90 độ ( góc nt chắn nửa đt)
góc BEC = 90 độ ( góc nt chắn 1/2 đt)
Tứ giác BDEC có hai đỉnh kề D và E cùng nhìn BC dưới một góc vuông . Do đó tứ giác BDEC nt
suy ra góc BDE + góc BCE = 180 độ (1)
Mặt khác : góc ADE + góc BDE = 180 độ ( kề bù ) (2)
(1) (2) suy ra góc ADE = góc ACB
Xét tam giác ADE và tam giác ACB có
goc BAC chung
goc ADE = góc BAC (cmt)
suy ra tam giác ADE đồng dạng tam giác ACB (g.g)
nên AD/AC = AE/AB
hay AD.AB =AE.AC.

a:
Xét đường tròn đường kính HB có
ΔHMB nội tiếp đường tròn
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét đường tròn đường kính HC có
ΔHNC nội tiếp đường tròn
HC là đường kính
Do đó: ΔHNC vuông tại N
Xét tứ giác AMHN có
\(\widehat{NAM}=\widehat{ANH}=\widehat{AMH}=90^0\)
nên AMHN là hình chữ nhật
b: \(BC=\sqrt{6^2+8^2}=10\)(cm)
=>AH=6*8/10=4,8(cm)
=>MN=4,8(cm)
c: góc EMN=góc EMH+góc NMH
=góc EHM+góc NAH
=góc HAC+góc HCA=90 độ
=>MN là tiếp tuyến của (E)