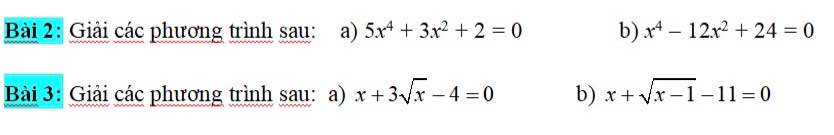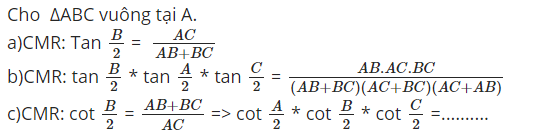Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(4,=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{\left(\sqrt{2}-\sqrt{3}\right)^2-9}=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{-4-2\sqrt{6}}=\dfrac{3\sqrt{3}-3\sqrt{2}+9}{2+\sqrt{6}}\\ =\dfrac{\left(3\sqrt{3}-3\sqrt{2}+9\right)\left(\sqrt{6}-2\right)}{2}\\ =\dfrac{9\sqrt{2}-6\sqrt{3}-6\sqrt{3}+6\sqrt{2}+9\sqrt{6}-18}{2}\\ =\dfrac{15\sqrt{2}-12\sqrt{3}+9\sqrt{6}-18}{2}\)
\(c,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}=4\Leftrightarrow x-1=16\Leftrightarrow x=17\left(tm\right)\\ d,ĐK:x\ge-5\\ PT\Leftrightarrow\sqrt{x+5}=5\Leftrightarrow x+5=25\Leftrightarrow x=20\left(tm\right)\\ e,ĐK:x\ge0\\ PT\Leftrightarrow-2\sqrt{x}=-6\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ f,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x-1=1\Leftrightarrow x=2\left(tm\right)\)



2:
a: =>x^2(5x^2+2)+2=0
x^2>=0
5x^2+2>=2
=>x^2(5x^2+2)>=0 với mọi x
=>x^2(5x^2+2)+2>=2>0 với mọi x
=>PTVN
b: x^4-12x^2+24=0
=>x^4-12x^2+36-12=0
=>(x^2-6)^2-12=0
=>(x^2-6-2căn 3)(x^2-6+2căn 3)=0
=>x^2=6+2căn 3 hoặc x^2=6-2căn 3
=>\(x=\pm\sqrt{6+2\sqrt{3}};x=\pm\sqrt{6-2\sqrt{3}}\)

1,\(\sqrt{\left(x-1\right)^2}=\left|x-1\right|=-\left(x-1\right)=1-x\)
2,\(\sqrt{\left(a-2b\right)^2}=\left|a-2b\right|=-\left(a-2b\right)=2b-a\)
3,\(\sqrt{\left(2x-1\right)^2}=\left|2x-1\right|=2x-1\)


a, Vì ME là tiếp tuyến đường tròn O và M là tiếp điểm
=> \(MO\perp MF\) ( t/c tiếp tuyến ) hay ^OME = 900
Vậy tam giác EMO là tam giác vuông tại M
b, mình sửa đề là OE = 60 cm nhé
Theo định lí Pytago cho tam giác EMO vuông tại M
\(ME=\sqrt{EO^2-OM^2}=48\)cm
c, sửa ON vuông OE tại N
đến đây thì mình chả hiểu đề kiểu gì, chịu, bạn chép đề kiểu gì ấy, sai tào lao sao á, xem lại nhé
a: Xét ΔMEO có \(\widehat{OME}=90^0\)
nên ΔMEO vuông tại M


a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+15^2=325\)
hay \(BC=5\sqrt{13}\left(cm\right)\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{15}{5\sqrt{13}}=\dfrac{3}{\sqrt{13}}\)
\(\Leftrightarrow\widehat{B}\simeq56^0\)
b: Xét ΔBAC có
BI là đường phân giác ứng với cạnh AC
nên \(\dfrac{AI}{AB}=\dfrac{CI}{BC}\)
hay \(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}\)
mà AI+CI=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}=\dfrac{AI+CI}{10+5\sqrt{13}}=\dfrac{15}{10+5\sqrt{13}}=\dfrac{-2+\sqrt{13}}{3}\)
Do đó: \(AI=\dfrac{-20+10\sqrt{13}}{3}\left(cm\right)\)


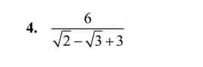
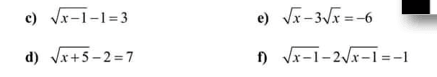



 Ai giúp mk vs ạ 🥲😞
Ai giúp mk vs ạ 🥲😞