Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Bảng biến thiên:
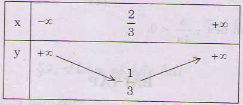
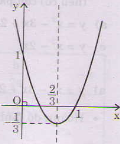
Đồ thị: - Đỉnh: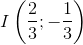 
- Trục đối xứng: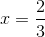 
- Giao điểm với trục tung A(0; 1)
- Giao điểm với trục hoành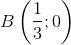 
, C(1; 0).
(hình dưới).
b) y = - 3x2 + 2x – 1=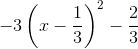 
Bảng biến thiên:
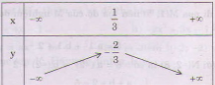
Vẽ đồ thị: - Đỉnh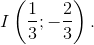 
Trục đối xứng: 
.
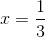- Giao điểm với trục tung A(0;- 1).
- Giao điểm với trục hoành: không có.
Ta xác định thêm mấy điểm: B(1;- 2), C(1;- 6). (bạn tự vẽ).
c) y = 4x2 - 4x + 1 =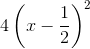 
.
Lập bảng biến thiên và vẽ tương tự câu a, b.
d) y = - x2 + 4x – 4 = - (x – 2)2
Bảng biến thiên:
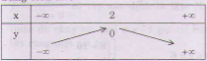
Cách vẽ đồ thị:
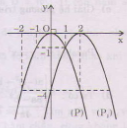
Ngoài cách vẽ như câu a, b, ta có thể vẽ như sau:
+ Vẽ đồ thị (P) của hàm số y = - x2.
+ Tịnh tiến (P) song song với Ox sang phải 2 đơn vị được (P1) là đồ thị cần vẽ. (hình dưới).
e) y = 2x2+ x + 1;
- Đỉnh I \(\left(\dfrac{-1}{4};\dfrac{-7}{8}\right)\)
- Trục đối xứng :\(x=\dfrac{-1}{4}\)
- Giao Ox: Đồ thị không giao với trục hoành
- Giao Oy: Giao với trục tung tại điểm (0;1)
Bảng biến thiên:
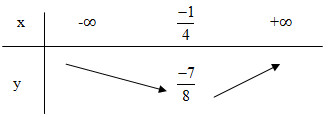
Vẽ đồ thị theo bảng sau:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 7 | 2 | 1 | 4 | 11 |
f) y = - x2 + x - 1.
- Đỉnh I \(\left(\dfrac{1}{2};\dfrac{-3}{4}\right)\)
- Trục đối xứng : \(x=\dfrac{1}{2}\)
- Giao Ox: Đồ thị không giao với trục hoành
- Giao Oy: Giao với trục tung tại điểm (0;-1)
Bảng biến thiên:
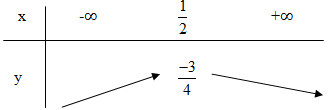
Vẽ đồ thị theo bảng sau:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -7 | -3 | -1 | -1 | -3 |
Vào thống kê của "Wall Duong" để xem đồ thị
a) 
b) Đỉnh I\(\left(\frac{3}{4};\frac{-1}{8}\right)\)trục đối xứng d: x=\(\frac{3}{4};a=2>0\)
Cho x=0 => y=1; y=1=> x=0,x=\(\frac{1}{2}\)
c) Ta có \(y=f\left(x\right)=2x^2-3\left|x\right|+1\)là hàm số chẵn, vì f(x)=f(-x) nên đồ thị đối xứng qua trục tung
Xét x>=0 thì y=2x2-3x+1 nên đồ thị y=f(x) lấy phần của prabol (P): y=2x2-3x+1 với x>=0 sau đó lấy phần đối xứng đó qua trục tung
Số nghiệm của phương trình 2x2-3|x|+1=m là số giao điểm của đồ thị y=f(x) với đường thẳng y=m
Phương trình vô nghiệm nếu m<\(-\frac{1}{8}\), có 2 nghiệm nếu \(\orbr{\begin{cases}m=\frac{-1}{8}\\m=1\end{cases}}\), có 3 nghiệm nếu m=1, có 4 nghiệm nếu \(-\frac{1}{8}< m< 1\)
1: Phương trình hoành độ giao điểm là
\(x^2-2x-1=x-1\)
=>x(x-3)=0
=>x=0 hoặc x=3
Khi x=0 thì y=-1
Khi x=3 thì y=2
2: Phương trình hoành độ giao điểm là:
\(-x+3=-x^2-4x+1\)
\(\Leftrightarrow x^2+3x+2=0\)
=>x=-1 hoặc x=-2
Khi x=-1 thì y=1+3=4
Khi x=-2 thì y=2+3=5
3: Phương trình hoành độ giao điểm là:
\(x^2-4x+4=2x-5\)
\(\Leftrightarrow x=3\)
=>y=1
Bài 1:
a: \(y=x^2-4x+3\)
Vì a=1>0 nên hàm số đồng biến khi \(x>-\dfrac{b}{2a}=\dfrac{4}{2}=2\) và nghịch biến khi x<2
Khi x=2 thì \(y=2^2-4\cdot2+3=4-8+3=-1\)
Bảng biến thiên:
Vẽ đồ thị:
b: \(y=-x^2+2x-3\)
Vì a=-1<0 nên hàm số đồng biến khi \(x< -\dfrac{b}{2a}=\dfrac{-2}{2\cdot\left(-1\right)}=1\) và nghịch biến khi x>1
Khi x=1 thì \(y=-1^2+2\cdot1-3=-1+2-3=-2\)
Bảng biến thiên:
Vẽ đồ thị:
c: \(y=x^2+2x\)
Vì a=1>0 nên hàm số đồng biến khi \(x>-\dfrac{b}{2a}=\dfrac{-2}{2}=-1\); hàm số nghịch biến khi x<-1
Khi x=-1 thì \(y=\left(-1\right)^2+2\cdot\left(-1\right)=1-2=-1\)
Bảng biến thiên:
vẽ đồ thị:
d: \(y=-2x^2-2\)
Vì a=-2<0
nên hàm số đồng biến khi \(x< -\dfrac{b}{2a}=0\) và nghịch biến khi x>0
Khi x=0 thì \(y=-2\cdot0^2-2=-2\)
Bảng biến thiên:
Vẽ đồ thị:
chữ xấu quá e. xấu hơn a hồi trc :))