
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)

\({x^2} = {4^2} + {2^2} = 20 \Rightarrow x = 2\sqrt 5 \)
\({y^2} = {5^2} - {4^2} = 9 \Leftrightarrow y = 3\)
\({z^2} = {\left( {\sqrt 5 } \right)^2} + {\left( {2\sqrt 5 } \right)^2} = 25 \Rightarrow z = 5\)
\({t^2} = {1^2} + {2^2} = 5 \Rightarrow t = \sqrt 5 \)

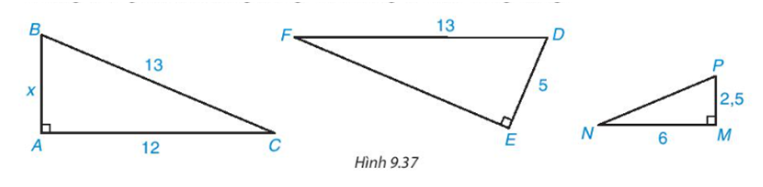
Những tam giác đồng dạng là
- Tam giác ABC đồng dạng với tam giác EDF với tỉ số đồng dạng là 1
- Tam giác MPN đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\frac{1}{2}\)
- Tam giác MPN đồng dạng với tam giác EDF với tỉ số đồng dạng là \(\frac{1}{2}\)


a.
\(A=\left(\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+x+1}{x}+\dfrac{x+2}{x}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+3x+1}{x}\right).\dfrac{x}{x+1}\)
\(=\dfrac{x^2+3x+1}{x+1}\)
2.
\(x^3-4x^3+3x=0\Leftrightarrow x\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=1\left(loại\right)\\x=3\end{matrix}\right.\)
Với \(x=3\Rightarrow A=\dfrac{3^2+3.3+1}{3+1}=\dfrac{19}{4}\)



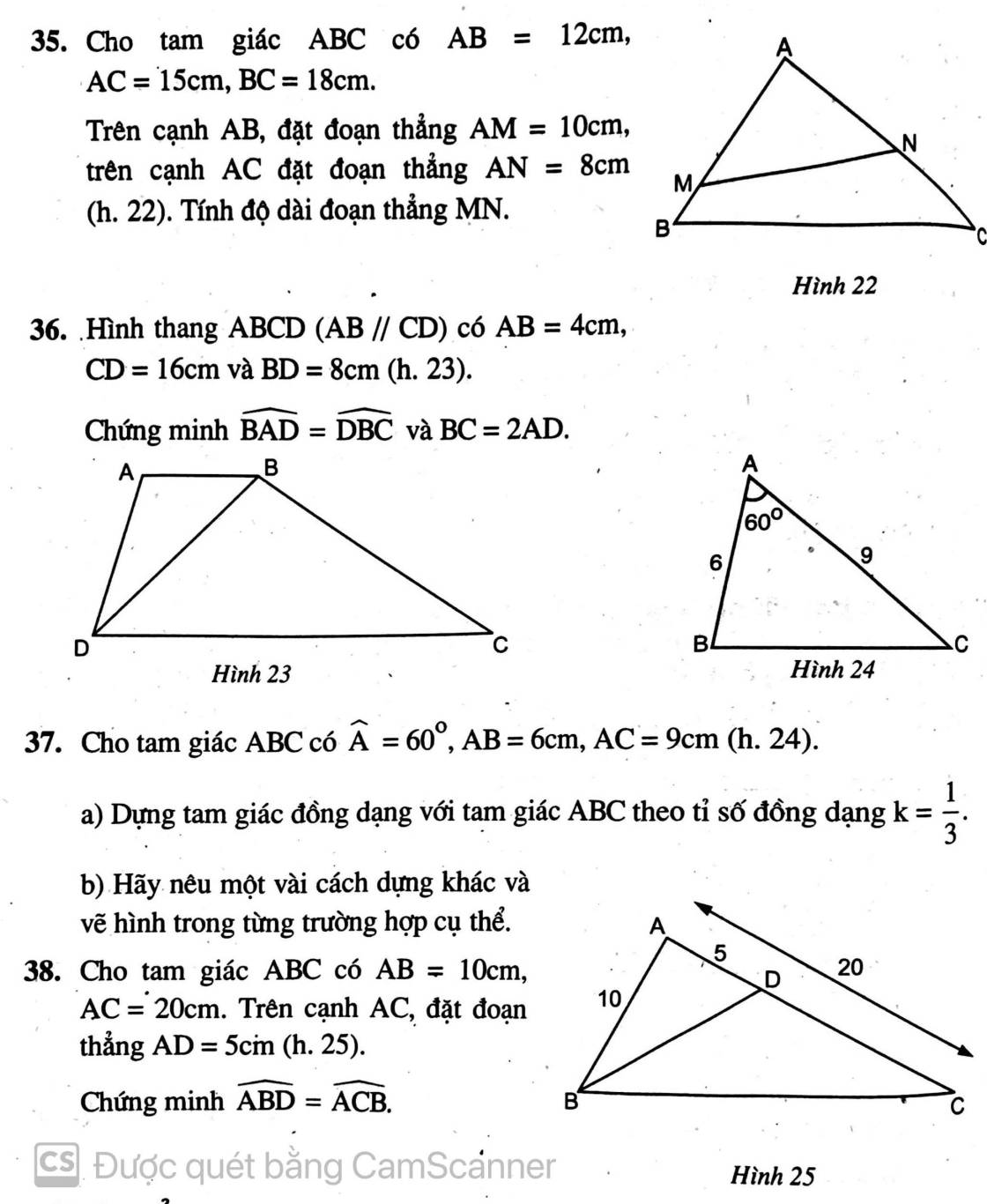
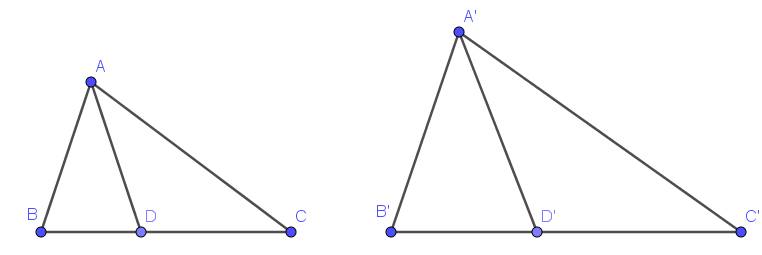
Bài 4:
a. Vì $\triangle ABC\sim \triangle A'B'C'$ nên:
$\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}(1)$ và $\widehat{ABC}=\widehat{A'B'C'}$
$\frac{DB}{DC}=\frac{D'B'}{D'C}$
$\Rightarrow \frac{BD}{BC}=\frac{D'B'}{B'C'}$
$\Rightarrow \frac{BD}{B'D'}=\frac{BC}{B'C'}(2)$
Từ $(1); (2)\Rightarrow \frac{BD}{B'D'}=\frac{BC}{B'C'}=\frac{AB}{A'B'}$
Xét tam giác $ABD$ và $A'B'D'$ có:
$\widehat{ABD}=\widehat{ABC}=\widehat{A'B'C'}=\widehat{A'B'D'}$
$\frac{AB}{A'B'}=\frac{BD}{B'D'}$
$\Rightarrow \triangle ABD\sim \triangle A'B'D'$ (c.g.c)
b.
Từ tam giác đồng dạng phần a và (1) suy ra:
$\frac{AD}{A'D'}=\frac{AB}{A'B'}=\frac{BC}{B'C'}$
$\Rightarrow AD.B'C'=BC.A'D'$



.png)
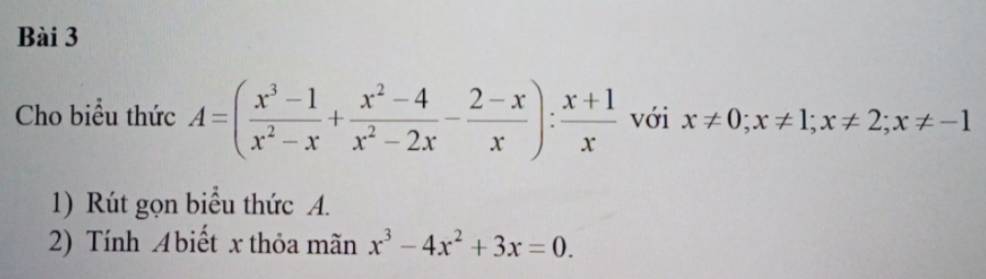



3:
a: Xét ΔACH vuông tại H và ΔBCA vuông tại A có
góc C chung
=>ΔACH đồng dạng vơi ΔBCA
b: Xét ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC