Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

thi cấp tỉnh mà có bài là quá ngon rồi !
Áp dụng BĐT \((a+b+c)^2 \geq 3(ab+bc+ca)\) ta có:
\(\left(\dfrac{xy}{z}+\dfrac{xz}{y}+\dfrac{yz}{x}\right)^2 \geq 3(x^2+y^2+z^2)=9\)
\(\Leftrightarrow \dfrac{xy}{z}+\dfrac{xz}{y}+\dfrac{yz}{x} \geq 3\)
Đẳng thức xảy ra khi \(x=y=z=1\)

Ta có:
\(GT\Leftrightarrow2-3x^2=2\left(y+z\right)^2-2yz\ge2\left(y+z\right)^2-\dfrac{1}{4}.2\left(y+z\right)^2=\dfrac{3\left(y+z\right)^2}{2}\)(AM-GM)
\(\Rightarrow4-6x^2\ge3\left(y+z\right)^2\Leftrightarrow4\ge3\left[2x^2+\left(y+z\right)^2\right]\)
Áp dụng BĐT bunyakovsky: \(\left(1+2\right)\left[2x^2+\left(y+z\right)^2\right]\ge2\left(x+y+z\right)^2\)
\(\Rightarrow\left(x+y+z\right)^2\le2\Leftrightarrow-\sqrt{2}\le x+y+z\le\sqrt{2}\)
Vậy \(P_{Min}=-\sqrt{2}\) khi \(x=y=z=\dfrac{-\sqrt{2}}{3}\);\(P_{Max}=\sqrt{2}\)khi \(x=y=z=\dfrac{\sqrt{2}}{3}\)

\(\sqrt{1-x-2x^2}=\sqrt{\left(1+x\right)\left(1-2x\right)}\le\dfrac{1+x-2x+1}{2}=\dfrac{-x+2}{2}\)
(AM-GM)
do đó \(A\le\dfrac{x}{2}+\dfrac{-x+2}{2}=1\)
Dấu = xảy ra khi 1+x=1-2x <=> x=0 (tmđk)

Xét phương trình hoành độ giao điểm của (d) và (p):
\(x^2=x+m-1\)
\(\Leftrightarrow x^2-x-m+1=0\left(1\right)\)
Xét phương trình (1) có:
\(\Delta=\left(-1\right)^2-4\left(-m+1\right)=4m-3\)
Để (d) cắt (p) tại 2 điểm thì phương trình (1) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta>0\Leftrightarrow4m-3>0\Leftrightarrow m>\dfrac{3}{4}\)
Áp dụng hệ thức Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=1\\x_1.x_2=1-m\end{matrix}\right.\)
Theo đề bài ta có:
\(4\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{4\left(x_1+x_2\right)}{x_1x_2}-x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{4}{1-m}-\left(1-m\right)+3=0\left(m\ne1\right)\)
\(\Leftrightarrow4-\left(1-m\right)^2+3\left(1-m\right)=0\)
\(\Leftrightarrow m^2+m-6=0\)
\(\Leftrightarrow\left(m-2\right)\left(m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-2=0\\m+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\left(tm\right)\\m=-3\left(ktm\right)\end{matrix}\right.\)
Vậy để (d)cắt (p) tại 2 điểm có hoành độ \(x_1,x_2\) thỏa mãn \(4\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+3=0\) thì m=2

1, đk: \(x>0\) và \(x\ne4\)
Ta có: A=\(\dfrac{1}{2\sqrt{x}-x}=\dfrac{1}{-\left(x-2\sqrt{x}+1\right)+1}=\dfrac{1}{-\left(\sqrt{x}-1\right)^2+1}\)
Ta luôn có: \(-\left(\sqrt{x}-1\right)^2\le0\) với \(x>0\) và \(x\ne4\)
\(\Rightarrow-\left(\sqrt{x}-1\right)^2+1\le1\)
\(\Rightarrow A\ge1\). Dấu "=" xảy ra <=> x=1 (t/m)
Vậy MinA=1 khi x=1
2, đk: \(x\ge0;x\ne1;x\ne9\)
Ta có: B=\(\dfrac{1}{x-4\sqrt{x}+3}=\dfrac{1}{\left(x-4\sqrt{x}+4\right)-1}=\dfrac{1}{\left(\sqrt{x}-2\right)^2-1}\)
Ta luôn có: \(\left(\sqrt{x}-2\right)^2\ge0\) với \(x\ge0;x\ne1;x\ne9\)
\(\Rightarrow\left(\sqrt{x}-2\right)^2-1\ge-1\)
\(\Rightarrow B\le-1\). Dấu "=" xảy ra <=> x=4 (t/m)
Vậy MaxB=-1 khi x=4
3, đk: \(x\ge0;x\ne15+4\sqrt{11}\)
Ta có: C=\(\dfrac{1}{4\sqrt{x}-x+7}=\dfrac{1}{-\left(x-4\sqrt{x}+4\right)+11}=\dfrac{1}{-\left(\sqrt{x}-2\right)^2+11}\)
Ta luôn có: \(-\left(\sqrt{x}-2\right)^2\le0\) với \(x\ge0;x\ne15+4\sqrt{11}\)
\(\Rightarrow-\left(\sqrt{x}-2\right)^2+11\le11\)
\(\Rightarrow C\ge\dfrac{1}{11}\). Dấu "=" xảy ra <=> x=4 (t/m)
Vậy MinC=\(\dfrac{1}{11}\) khi x=4

(x+y)2=x2+2xy+y2=1+ 2xy cái này phải phụ thuoc vào max hay min thì mới biệ luận tiếp

Ta có
a+1=a+a+b+c>= 4căn4 a^2bc
b+1=b+..........>=.........ab^2c
c+1=c...........>=..........abc^2
=> (a+1)(b+1)(c+1)/abc>= 64abc/abc ( nhân cho 1/abc)
=>(a+1)(b+1)(c+1)/abc >= 64 ( đpcm)
Chúc bạn học tốt!![]()

\(\dfrac{x^2}{\sqrt{1-x^2}}=\dfrac{x^3}{x\sqrt{1-x^2}}=\dfrac{x^3}{\sqrt{x^2}.\sqrt{1-x^2}}\ge\dfrac{x^3}{\dfrac{x^2+1-x^2}{2}}=2x^3\)
\(\dfrac{y^2}{\sqrt{1-y^2}}=\dfrac{y^3}{y\sqrt{1-y^2}}=\dfrac{y^3}{\sqrt{y^2}.\sqrt{1-y^2}}\ge\dfrac{y^3}{\dfrac{y^2+1-y^2}{2}}=2y^3\)
\(\dfrac{z^2}{\sqrt{1-z^2}}=\dfrac{z^3}{z\sqrt{1-z^2}}=\dfrac{z^3}{\sqrt{z^2}.\sqrt{1-z^2}}\ge\dfrac{z^3}{\dfrac{z^2+1-z^2}{2}}=2z^3\)
Cộng từng vế của các BĐT , ta được :
\(\dfrac{x^2}{\sqrt{1-x^2}}+\dfrac{y^2}{\sqrt{1-y^2}}+\dfrac{z^2}{\sqrt{1-z^2}}\ge2\left(x^3+y^3+z^3\right)=2\)
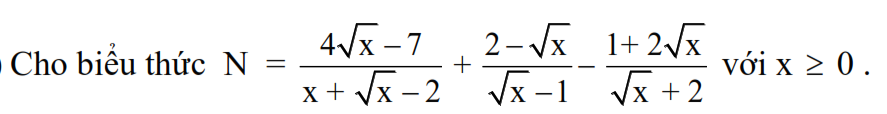
a: Ta có: \(N=\dfrac{4\sqrt{x}-7}{x+\sqrt{x}-2}+\dfrac{2-\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{4\sqrt{x}-7+4-x-2x+\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-3x+5\sqrt{x}-4}{x+\sqrt{x}-2}\)