Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
y
=
3
sin
x
+
4
cos
x
+
5
⇔
3
sin
x
+
4
cos
x
+
5
−
y
=
0
Để phương trình có nghiệm thì 3 2 + 4 2 ≥ 5 − y 2
⇔
25
≥
25
−
10
y
+
y
2
⇔
y
2
−
10
y
≤
0
⇔
0
≤
y
≤
10
Vậy giá trị nhỏ nhất của hàm số là 0.
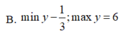
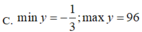
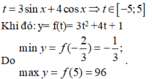
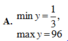
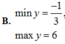
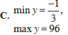
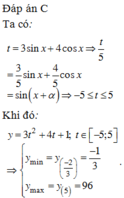

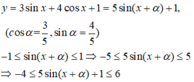
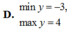

Lời giải:
Đặt \(3\sin x+4\cos x=t\)
Áp dụng BĐT Bunhiacopxky:
\(t^2=(3\sin x+4\cos x)^2\leq (3^2+4^2)(\sin ^2x+\cos ^2x)=25\)
\(\Rightarrow -5\leq t\leq 5\)
Với $t\in [-5;5]$ ta có:
\(y=3t^2+4t+1\leq 3.25+4.5+1=96\)
Mặt khác: \(y=3t^2+4t+1=3(t+\frac{2}{3})^2-\frac{1}{3}\)
\((t+\frac{2}{3})^2\geq 0, \forall t\in [-5;5]\Rightarrow y\geq -\frac{1}{3}\)
Vậy \(y_{\min}=\frac{-1}{3}; y_{\max}=96\)