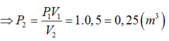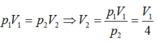Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quá trình đẳng nhiệt: \(p\sim\dfrac{1}{V}\)
Theo định luật Bôi-lơ Ma-ri-ốt ta có:
\(p_1\cdot V_1=p_2\cdot V_2\)
\(\Rightarrow V_2=\dfrac{p_1\cdot V_1}{p_2}=\dfrac{2\cdot12}{4}=6l\)
Chọn B

Áp dụng định luật Bôi lơ - Ma ri ốt có:
`p_1.V_1=p_2.V_2`
`=>4.V_2=9.3`
`=>V_2=6,75(l)`
Ta có
\(\dfrac{p_1}{V_1}=\dfrac{p_2}{V_2}\\ \Rightarrow V_1=\dfrac{p_1V_2}{p_2}=1,\left(3\right)l\)

Tóm tắt đề bài như sau:
\(\left\{{}\begin{matrix}V=10\left(l\right)\\p=2\left(atm\right)\\T=87+273=360\left(K\right)\end{matrix}\right.\underrightarrow{Đẳngáp}\left\{{}\begin{matrix}V_1=?\\p_1=2\left(atm\right)\\T_1=\dfrac{T}{2}=180\left(K\right)\end{matrix}\right.\) \(\underrightarrow{Đẳngnhiet}\left\{{}\begin{matrix}V_2=?\\p_2=0,5\left(atm\right)\\T_2=180\left(K\right)\end{matrix}\right.\)
Phương trình trạng thái khí lí tưởng ( Claperon Mendeleep ): \(\dfrac{pV}{T}=const\)
Đẳng áp: \(\dfrac{V}{T}=\dfrac{V_1}{T_1}\Leftrightarrow V_1=\dfrac{10.180}{360}=5\left(l\right)\)
Đẳng nhiệt: \(p_1V_1=p_2V_2\Rightarrow V_2=\dfrac{p_1V_1}{p_2}=\dfrac{2.5}{0,5}=20\left(l\right)\)
Vậy thể tích sau cùng của khối khí trên là V2=20(l)

Đáp án A
Vì nhiệt độ của khối khí được giữ không đổi trong suốt quá trình nén, nên theo định thức bôi-lơ-ma-ri-ốt ta có:
![]()