K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
0
NH
3
21 tháng 3 2016
\(C=\frac{5^2}{1.6}+\frac{5^2}{6.11}+...+\frac{5^2}{26.31}\)
\(=5.\left(\frac{5}{1.6}+\frac{5}{6.11}+...+\frac{5}{26.31}\right)\)
\(=5.\left(1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+...+\frac{1}{26}-\frac{1}{31}\right)\)
\(=5.\left(1-\frac{1}{31}\right)\)
\(=5.\frac{29}{31}\)
\(=\frac{145}{31}\)
28 tháng 4 2016
Ta có S=\(\frac{1+2+2^2+...+2^{2015}}{1-2^{2016}}\)
Đặt M là tử của 2 ta có
M=1+2+2^2+...+2^2015
2M=2*(1+2+2^2+...+2^2015)
2M=2+2^2+2^3+...+2^2016
2M-M=(2+2^2+2^3+...+2^2016)-(1+2+2^2+...+2^2015)
M=2^2016-1
S=\(\frac{2^{2016}-1}{1-2^{2016}}\)
Ta thấy tử và mẫu của S là 2 số đối nhau.Mà 2 số đối nhau luôn có thương là -1
Nên S=-1
HA
cho biểu thức C = 4 + 4 mũ 2 + 4 mũ 3 + .....+ 4 mũ 2021 + 4 mũ 2022
chức minh rằng C chia hết cho 5
1
KV
4 tháng 11 2023
\(C=4+4^2+4^3+...+4^{2021}+4^{2022}\)
\(=\left(4+4^2\right)+\left(4^3+4^4\right)+...+\left(4^{2021}+4^{2022}\right)\)
\(=4.\left(1+4\right)+4^3.\left(1+4\right)+...+4^{2021}.\left(1+4\right)\)
\(=4.5+4^3.5+...+4^{2021}.5\)
\(=5.\left(4+4^3+...+4^{2021}\right)⋮5\)
Vậy \(C⋮5\)
22 tháng 4 2016
giải luôn; đặt A=1/2^2+1/3^2+...+1/8^2
1/2^2 < 1/1.2
1/3^2<1/2.3
.......
1/8^2<1/7.8
=> 1/2^2 + 1/3^2 +...+1/8^2<1/1.2 + 1/2.3 + ....+ 1/7.8
=>A<1-1/2 + 1/2 - 1/3 + ....+1/7-1/8
=>A<1-1/8<1
vậy 1/2^2+1/3^2+....+1/8^2 <1
like nha 
BH
1
2 tháng 3 2016
1 nâng lên lũy thừa nào cũng bằng 1, do đó:
\(1^6=1^{12}=1^{20}=1^{30}=1^{40}=1^3\)
\(\Rightarrow A=1+1+1+1+1=5;B=1\)
\(5>1\Rightarrow A>B\)
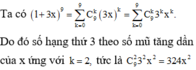
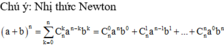
1 + 2 + 2² + 2³ + ... + 2ˣ⁺³ = 1023
Đặt A = 1 + 2 + 2² + ... + 2ˣ⁺³
⇒ 2A = 2 + 2² + 2³ + ... + 2ˣ⁺⁴
⇒ A = 2A - A
= (2 + 2² + 2³ + ... + 2ˣ⁺⁴) - (1 + 2 + 2² + ... + 2ˣ⁺³)
= 2ˣ⁺⁴ - 1
A = 1023
⇒ 2ˣ⁺⁴ - 1 = 1023
⇒ 2ˣ⁺⁴ = 1023 + 1
2ˣ⁺⁴ = 1024
⇒ 2ˣ⁺⁴ = 2¹⁰
⇒ x + 4 = 10
⇒ x = 10 - 4
⇒ x = 6