Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Bài 1:
Ta nhớ công thức \(\sin^2x=\frac{1-\cos 2x}{2}\). Áp dụng vào bài toán:
\(F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx\)
\(\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})\)
\(\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c\)
Giải thích 1 chút: \(d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx\)
Vì \(F(0)=8\Rightarrow -1+c=8\Rightarrow c=9\)
\(\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9\)
Câu 2:
Áp dụng nguyên hàm từng phần như bài bạn đã đăng:
\(\Rightarrow F(x)=-xe^{-x}-e^{-x}+c\)
Vì \(F(0)=1\Rightarrow -1+c=1\Rightarrow c=2\)
\(\Rightarrow F(x)=-e^{-x}(x+1)+2\), tức B là đáp án đúng
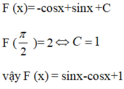
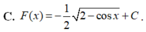


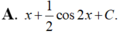
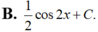
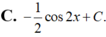
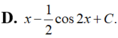
Từ sau khi đăng bài phiền bạn học cách gõ công thức toán, nhìn ntn rất rối mắt
1)
\(A=-\int\cot^2 xdx=-\int\frac{\cos ^2x}{\sin^2x}dx=-\int \frac{1-\sin^2x}{\sin^2x}dx=-\int\frac{dx}{\sin^2x}+\int dx\)
\(\Rightarrow A=\cot x+x+c\)
2)
\(B=\int xe^{-x}dx\). Đặt \(\left\{\begin{matrix} u=x\\ dv=e^{-x}dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=dx\\ v=\int e^{-x}dx=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow B=-xe^{-x}+\int e^{-x}dx=-xe^{-x}-e^{-x}+c\)
Bài 3: Ta có
\(F(x)=\int f(x)dx=\int (2x+\sin x+2\cos x)dx=2\int xdx+\int \sin xdx+2\int \cos xdx\)
\(\Leftrightarrow F(x)=x^2-\cos x+2\sin x+c\)
Vì \(F(0)=1\Rightarrow 0-1+0+c=1\Leftrightarrow c=2\)
\(\Rightarrow F(x)=x^2-\cos x+2\sin x+2\), tức đáp án A là đáp án đúng.
P/s: Mấy bải này rất dễ. Mình nghĩ cơ bản là bạn nên học thuộc bảng đạo hàm và tính chất nguyên hàm là sẽ ổn thôi.