Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

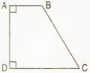
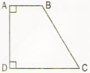
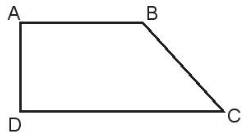
Quan sát hình vẽ để tìm các cặp cạnh vuông góc với nhau, các cặp cạnh cắt nhau mà không vuông góc với nhau.
Lời giải chi tiết:
a) AD và AB là cặp cạnh vuông góc với nhau.
AD và DC là cặp cạnh vuông góc với nhau.
b) AB và BC cắt nhau mà không vuông góc với nhau.
BC và CD cắt nhau mà không vuông góc với nhau.
đúng k bạn ?

a) AD và AB là cặp cạnh vuông góc với nhau.
AD và DC là cặp cạnh vuông góc với nhau.
b) AB và BC cắt nhau mà không vuông góc với nhau
BC và CD cắt nhau mà không vuông góc với nhau.

a) AD và AB là cặp cạnh vuông góc với nhau.
AD và DC là cặp cạnh vuông góc với nhau.
b) AB và BC cắt nhau mà không vuông góc với nhau
BC và CD cắt nhau mà không vuông góc với nhau.

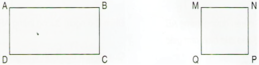
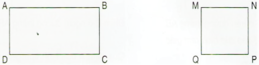
a) Trong hình chữ nhật ABCD có:
- AB và DC là cặp cạnh song song với nhau.
- AD và BC là cặp cạnh song song với nhau.
b) Trong hình vuông MNPQ có:
- MN và PQ là cặp cạnh song song với nhau.
- MQ và NP là cặp cạnh song song với nhau.

Trong hình chữ nhật ABCD có:
- AB và DC là cặp cạnh song song với nhau.
- AD và BC là cặp cạnh song song với nhau.
Trong hình vuông MNPQ có:
- MN và PQ là cặp cạnh song song với nhau.
- MQ và NP là cặp cạnh song song với nhau.

a) Các cặp cạnh vuông góc với nhau trong hình trên là: AB và AD ; DA và DC
b) Các cặp cạnh cắt nhau mà không vuông góc với nhau là: AB và BC; BC và CD

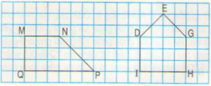
MP và MN, MN và NQ, NQ và PQ, PQ và MP, MP và MH, NQ và NK

a) MN song song với QP.
DI song song với GH
b) MN vuông góc với MQ.
DE vuông góc với EG
DI vuông góc với IH
IH vuông góc với GH
MQ vuông góc với QP

a) cặp cạnh vuông góc là: BA,EA.
cặp cạnh song song là: AB,ED.
mik chỉ bt như vậy thôi mong bạn tick cho mik.
Qua hình vẽ, ta được:
a) Các cặp cạnh vuông góc với nhau: $AB$ và $AE$; $AD$ và $DE$
Các cặp cạnh song song với nhau: $AB$ và $DE$
b) Các cặp cạnh cắt nhau mà không vuông góc với nhau: $AB$ và $BC$; $BC$ và $CD$; $CD$ và $DE$