Mng giúp em vs ah
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 6:
a: Xét ΔAPC có
M là trung điểm của AC
Q là trung điểm của PC
Do đó: MQ là đường trung bình của ΔAPC
Suy ra: MQ//AP
Xét ΔBMQ có
P là trung điểm của BQ
PD//MQ
Do đó: D là trung điểm của BM
Suy ra: DB=DM

a: Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
Do đó: \(\widehat{ABC}=\widehat{ECN}\)
Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
BD=CE
\(\widehat{MBD}=\widehat{NCE}\)
Do đó: ΔMBD=ΔNCE
=>DM=EN
b: Ta có: DM\(\perp\)BC
EN\(\perp\)BC
Do đó: DM//EN
Xét ΔIDM vuông tại D và ΔIEN vuông tại E có
MD=EN
\(\widehat{MDI}=\widehat{ENC}\)(hai góc so le trong, DM//EN)
Do đó: ΔIDM=ΔIEN
=>IM=IN
=>I là trung điểm của MN

Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$

Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k$
$\Rightarrow a=bk, c=dk$. Khi đó:
$\frac{a-b}{b}=\frac{bk-b}{b}=\frac{b(k-1)}{b}=k-1(1)$
$\frac{c-d}{d}=\frac{dk-d}{d}=\frac{d(k-1)}{d}=k-1(2)$
Từ $(1); (2)\Rightarrow \frac{a-b}{b}=\frac{c-d}{d}$
-------------------
$\frac{2a+3b}{2a-3b}=\frac{2bk+3b}{2bk-3b}=\frac{b(2k+3)}{b(2k-3)}=\frac{2k+3}{2k-3}(3)$
$\frac{2c+3d}{2c-3d}=\frac{2dk+3d}{2dk-3d}=\frac{d(2k+3)}{d(2k-3)}=\frac{2k+3}{2k-3}(4)$
Từ $(3); (4)\Rightarrow \frac{2a+3b}{2a-3b}=\frac{2c+3d}{2c-3d}$

a.\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\);\(ĐK:x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(A=\dfrac{1}{\left(x-1\right)}-\dfrac{2x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)\left(x^2+1\right)}\)
\(A=\dfrac{1}{x-1}-\dfrac{2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x-1}{x^2+1}\)
b.\(A=0,2=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow x^2+1=5x-5\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
c.\(A< 0\) mà \(x^2+1\ge1>0\)
--> A<0 khi \(x-1< 0\)
\(\Leftrightarrow x< 1\)
a. -ĐKXĐ:\(x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{2}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{x^2+1}{\left(x^2+1\right)\left(x-1\right)}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\)
b. \(A=\dfrac{x-1}{x^2+1}=0,2\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{5\left(x-1\right)}{5\left(x^2+1\right)}=\dfrac{x^2+1}{5\left(x^2+1\right)}\)
\(\Rightarrow5x-5=x^2+1\)
\(\Leftrightarrow x^2-5x+1+5=0\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow x^2-2x-3x+6=0\)
\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=3\left(nhận\right)\end{matrix}\right.\)
c. \(A=\dfrac{x-1}{x^2+1}< 0\)
\(\Leftrightarrow x-1< 0\) (vì \(x^2+1>0\forall x\))
\(\Leftrightarrow x< 1\)

Sửa đề: \(\left(4-\dfrac{u}{2}\right)\left(\dfrac{u^2}{4}+2u+16\right)=4^3-\left(\dfrac{u}{2}\right)^3=64-\dfrac{u^3}{8}\)

1.
\(\dfrac{1-cosx+cos2x}{sin2x-sinx}=\dfrac{1-cosx+2cos^2x-1}{2sinx.cosx-sinx}\)
\(=\dfrac{cosx\left(2cosx-1\right)}{sinx\left(2cosx-1\right)}=\dfrac{cosx}{sinx}=cotx\)
2.
\(\dfrac{1+tan^4x}{tan^2x+cot^2x}=\dfrac{1+tan^4x}{tan^2x+\dfrac{1}{tan^2x}}=\dfrac{1+tan^4x}{\dfrac{tan^4x+1}{tan^2x}}=tan^2x\)
3.
\(sin^4x+cos^4x=sin^4x+cos^4x+2sin^2x.cos^2x-2sin^2x.cos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\)
\(=1-2sin^2x.cos^2x\)
4.
Áp dụng câu 3:
\(sin^4x+cos^4x=1-2sin^2x.cos^2x\)
\(=1-\dfrac{1}{2}\left(2sinx.cosx\right)^2\)
\(=1-\dfrac{1}{2}sin^22x\)
5.
\(sin\left(x+y\right)sin\left(x-y\right)=\dfrac{1}{2}cos\left[\left(x-y\right)-\left(x+y\right)\right]-\dfrac{1}{2}cos\left[\left(x-y\right)+\left(x+y\right)\right]\)
\(=\dfrac{1}{2}\left(cos2y-cos2x\right)=\dfrac{1}{2}\left(1-2sin^2y\right)-\dfrac{1}{2}\left(1-2sin^2x\right)\)
\(=sin^2x-sin^2y\)
6.
\(tanx+cotx=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}\)
\(=\dfrac{1}{sinx.cosx}=\dfrac{2}{2sinx.cosx}=\dfrac{2}{sin2x}\)

Bài 5:
Gọi độ dài quãng đường là x
Thời gian ô tô thứ nhất đi là x/40(h)
Thời gian ô tô thứ hai đi là x/50(h)
Theo đề, ta có: x/40-x/50=1,5
hay x=300

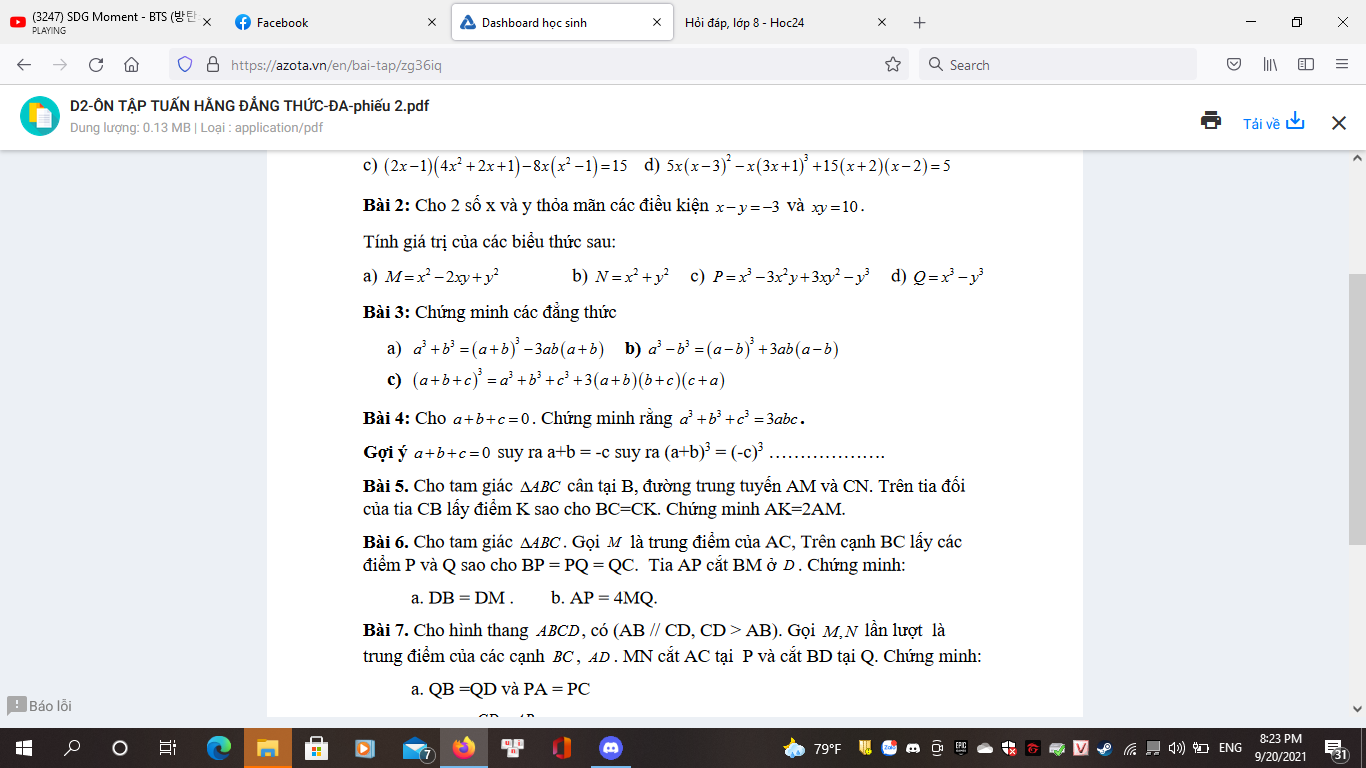 mng giúp mình bài 2 bài 3 bài 4 vs ah
mng giúp mình bài 2 bài 3 bài 4 vs ah


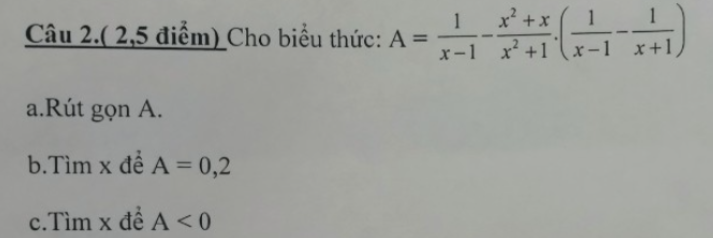
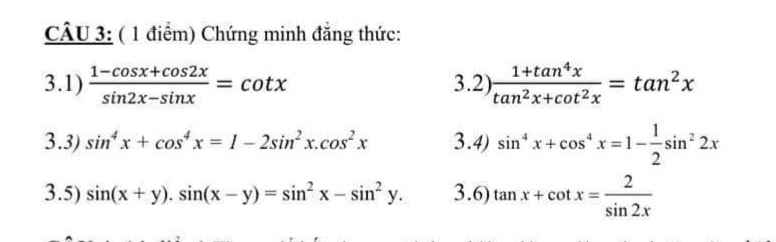

 giúp em vs mng ơi
giúp em vs mng ơi 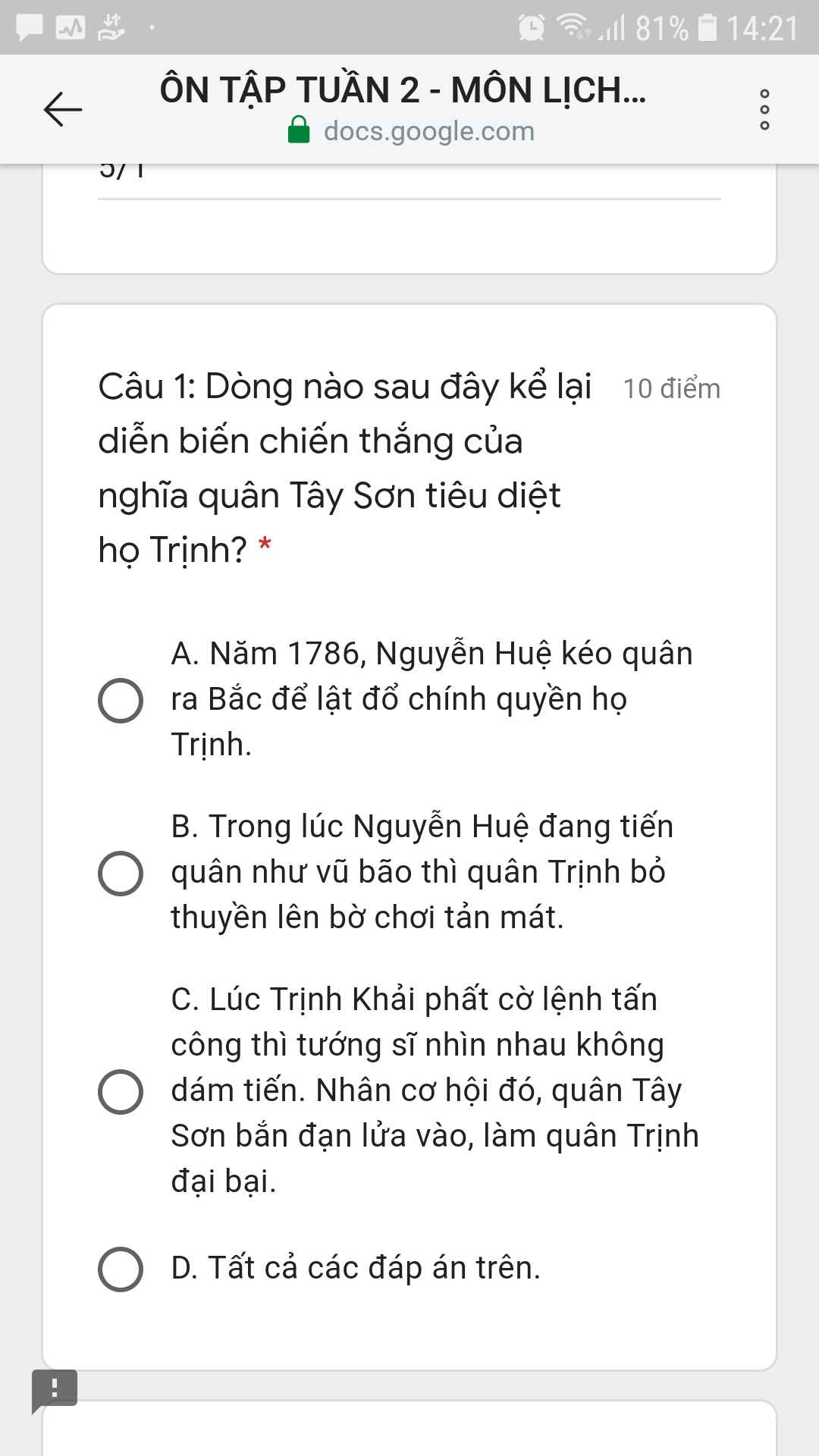
giúp gì vậy bạn
Olm chào em, hiện tại câu hỏi của em chưa hiển thị đấy có thể là do file mà em tải lên bị lỗi nên đã không hiển thị trên diễn đàn. Em nên viết đề bài trực tiếp trên Olm. Như vậy em sẽ không mắc phải lỗi file đề như vậy. Điều này giúp em nhanh chóng nhận được sự trợ giúp từ cộng đồng olm. Cảm ơn em đã đồng hành cùng Olm.