K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LB
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
1
30 tháng 9 2021
Bài 5:
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y-z}{2+3-4}=\dfrac{-20}{1}=-20\)
Do đó: x=-40; y=-60; z=-80
21 tháng 9 2021
\(2,\\ a,=7^{5+8}=7^{13}\\ b,=5^{8-5}=5^3\\ c,=\dfrac{1}{3^2}=\dfrac{1}{9}\\ d,=\dfrac{2^9}{2^{10}}=\dfrac{1}{2}\\ e,=\dfrac{3^9}{3^{12}}=\dfrac{1}{3^3}=\dfrac{1}{27}\\ f,=\dfrac{5^6}{5^3}=5^3=125\\ g,=\dfrac{\left(2\cdot3\right)^{12}\cdot2^2}{6^{11}}=\dfrac{6^{12}\cdot2^2}{6^{11}}=6\cdot4=24\\ h,=\dfrac{2^{18}\cdot3^{18}}{3^{18}\cdot2^{15}}=2^3=8\)
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
11 tháng 4 2022
Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5
30 tháng 7 2023
2:
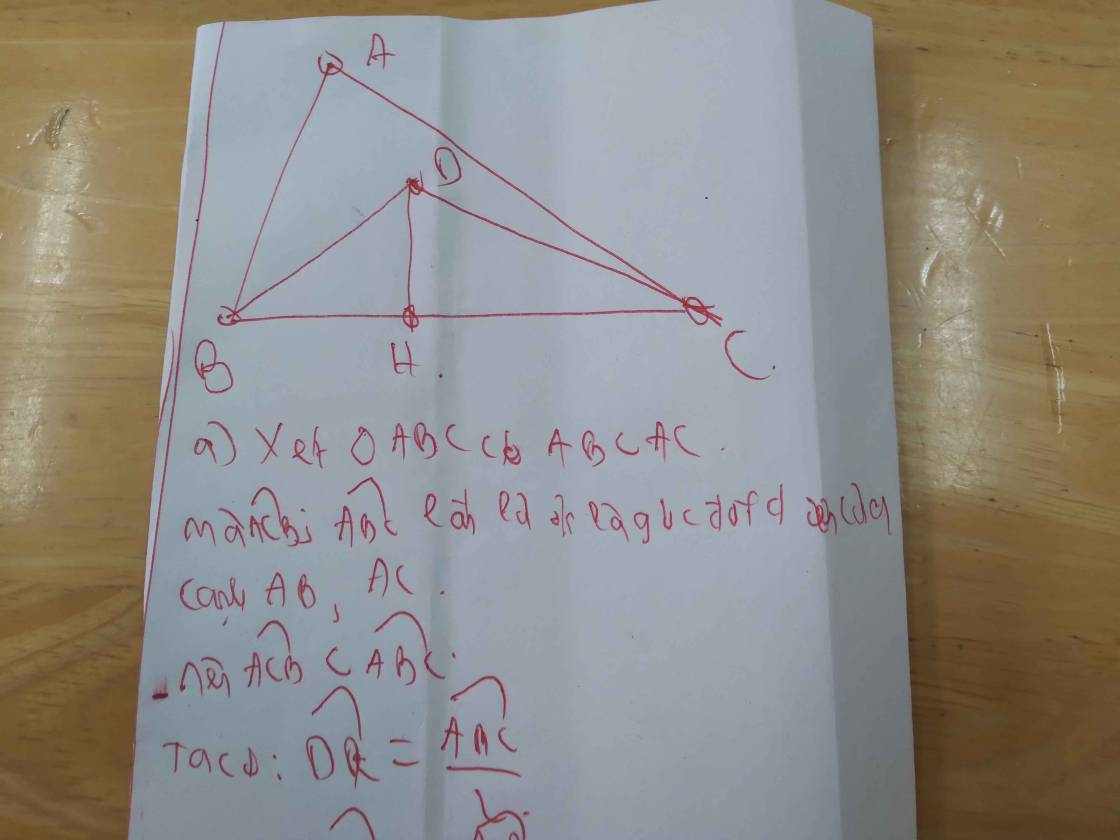
a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
=>ΔABD=ΔACD
b: ΔABD=ΔACD
=>góc ADB=góc ADC=180/2=90 độ
=>AD vuông góc BC
c: BC=12
=>BD=CD=6
AD=căn 10^2-6^2=8
d: BN=AB/2
CM=AC/2
mà AB=AC
nên BN=CM
Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>NC=BM
e: Xét ΔABC có
BM,CN là trung tuyến
BM cắt CN tại G
=>G là trọng tâm
=>A,G,D thẳng hàng và AG=2/3AD=16/3
5 tháng 7 2023
2:
a: A(x)=0
=>-5x+3=0
=>-5x=-3
=>x=3/5
b: B(x)=0
=>2x^3-18x=0
=>2x(x^2-9)=0
=>x(x-3)(x+3)=0
=>x=0;x=3;x=-3
c: C(x)=0
=>-x(-x-5)=0
=>x(x+5)=0
=>x=0 hoặc x=-5
d: D(x)=0
=>3x-3+2x^2-2x-x^2+2x-1=0
=>x^2+3x-4=0
=>x=-4 hoặc x=1
e: E(x)=0
=>2x^3-2x-x^2+1=0
=>2x(x^2-1)-(x^2-1)=0
=>(2x-1)(x-1)(x+1)=0
=>x=1/2;x=-1;x=1
4 tháng 12 2023
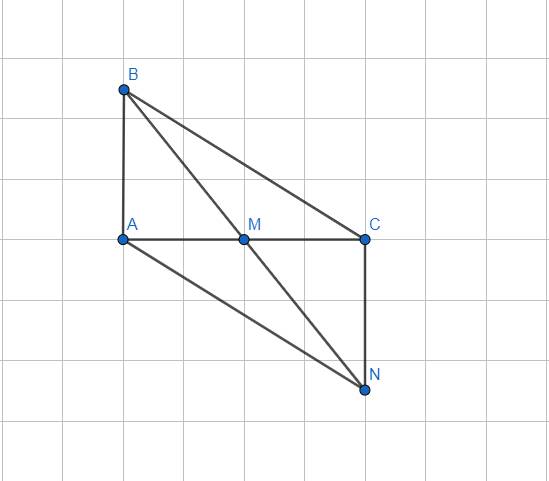
Xét ΔMAB và ΔMCN có
MA=MC
\(\widehat{AMB}=\widehat{CMN}\)
MB=MN
Do đó: ΔMAB=ΔMCN
=>AB=CN và \(\widehat{MAB}=\widehat{MCN}=90^0\)
=>CN\(\perp\)AC
Xét ΔMAN và ΔMCB có
MA=MC
\(\widehat{AMN}=\widehat{CMB}\)(hai góc đối đỉnh)
MN=MB
Do đó: ΔMAN=ΔMCB
=>AN=CB
ΔMAN=ΔMCB
=>\(\widehat{MAN}=\widehat{MCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//CB
1 tháng 12 2021
Gọi số công nhân 3 đội lần lượt là a,b,c(người;a,b,c∈N*)
Áp dụng tc dtsbn:
\(3a=4b=5c\Rightarrow\dfrac{a}{20}=\dfrac{b}{15}=\dfrac{c}{12}=\dfrac{a+b+c}{20+15+12}=\dfrac{47}{47}=1\\ \Rightarrow\left\{{}\begin{matrix}a=20\\b=15\\c=12\end{matrix}\right.\)
Vậy ...
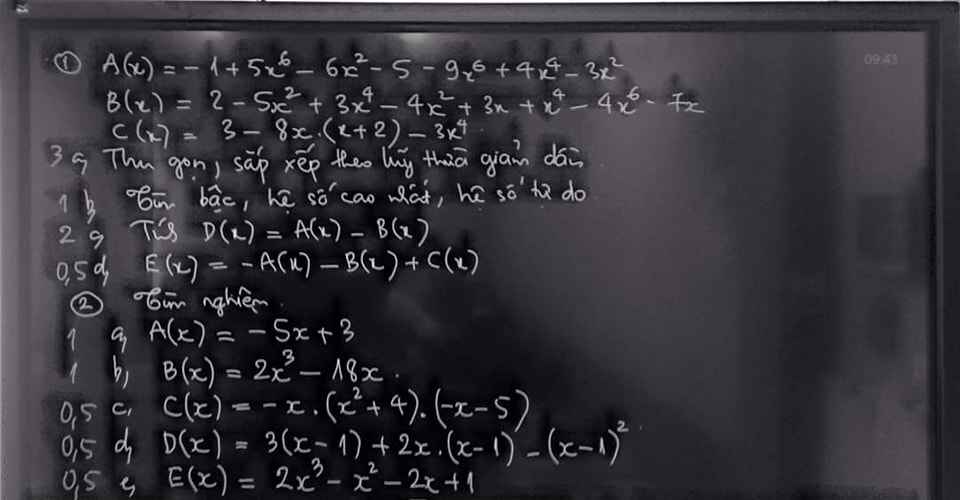
a: Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
Do đó: \(\widehat{ABC}=\widehat{ECN}\)
Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
BD=CE
\(\widehat{MBD}=\widehat{NCE}\)
Do đó: ΔMBD=ΔNCE
=>DM=EN
b: Ta có: DM\(\perp\)BC
EN\(\perp\)BC
Do đó: DM//EN
Xét ΔIDM vuông tại D và ΔIEN vuông tại E có
MD=EN
\(\widehat{MDI}=\widehat{ENC}\)(hai góc so le trong, DM//EN)
Do đó: ΔIDM=ΔIEN
=>IM=IN
=>I là trung điểm của MN