

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





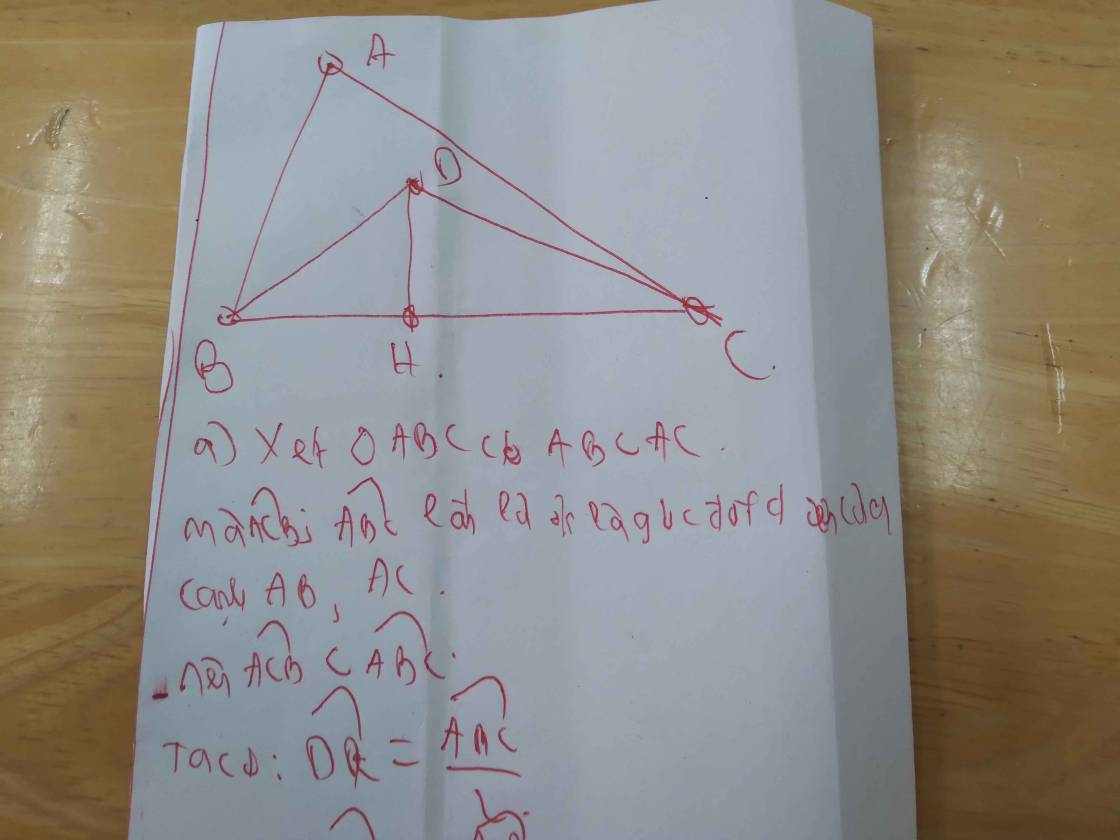
a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: AB=AM
=>A nằm trên đường trung trực của BM(1)
Ta có: DB=DM
=>D nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM

a: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
b: Xét ΔBME và ΔBAC có
góc BME=góc BAC
BM=BA
góc EBM chung
=>ΔBME=ΔBAC
=>BE=BC
=>ΔBEC cân tại B
Cho em hỏi với ạ: Tại sao lại khẳng định được BA = BM thế ạ;-;?

a) Các góc kề bù nhau là:
1. \(\widehat{xOy}\) và \(\widehat{xOt}\)
2. \(\widehat{yOz}\) và \(\widehat{zOt}\)
b) Ta có: \(\widehat{yOt}\) là góc bẹt \(\Rightarrow\widehat{yOt}=180^o\)
Mà \(\widehat{xOy}\) và \(\widehat{xOt}\) kề bù \(\Rightarrow\widehat{xOy}+\widehat{xOt}=\widehat{yOt}\)
\(\Rightarrow\widehat{xOt}=\widehat{yOt}-\widehat{xOy}=180^o-45^o=135^o\)
Ta có: \(\widehat{xOz}=\widehat{xOy}+\widehat{yOz}=45^o+30^o=75^o\)
Mà \(\widehat{yOz}\) và \(\widehat{zOt}\) kề bù \(\Rightarrow\widehat{yOz}+\widehat{zOt}=\widehat{yOt}=180^o\)
\(\Rightarrow\widehat{zOt}=\widehat{yOt}-\widehat{yOz}=180^o-30^o=150^o\)

ΔAED vuông tại E nên AE<AD
ΔDFC vuông tại F nên FC<DC
=>AE+FC<AD+DC=AC

a: Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
Do đó: \(\widehat{ABC}=\widehat{ECN}\)
Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
BD=CE
\(\widehat{MBD}=\widehat{NCE}\)
Do đó: ΔMBD=ΔNCE
=>DM=EN
b: Ta có: DM\(\perp\)BC
EN\(\perp\)BC
Do đó: DM//EN
Xét ΔIDM vuông tại D và ΔIEN vuông tại E có
MD=EN
\(\widehat{MDI}=\widehat{ENC}\)(hai góc so le trong, DM//EN)
Do đó: ΔIDM=ΔIEN
=>IM=IN
=>I là trung điểm của MN

Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5

2:
a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
=>ΔABD=ΔACD
b: ΔABD=ΔACD
=>góc ADB=góc ADC=180/2=90 độ
=>AD vuông góc BC
c: BC=12
=>BD=CD=6
AD=căn 10^2-6^2=8
d: BN=AB/2
CM=AC/2
mà AB=AC
nên BN=CM
Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>NC=BM
e: Xét ΔABC có
BM,CN là trung tuyến
BM cắt CN tại G
=>G là trọng tâm
=>A,G,D thẳng hàng và AG=2/3AD=16/3

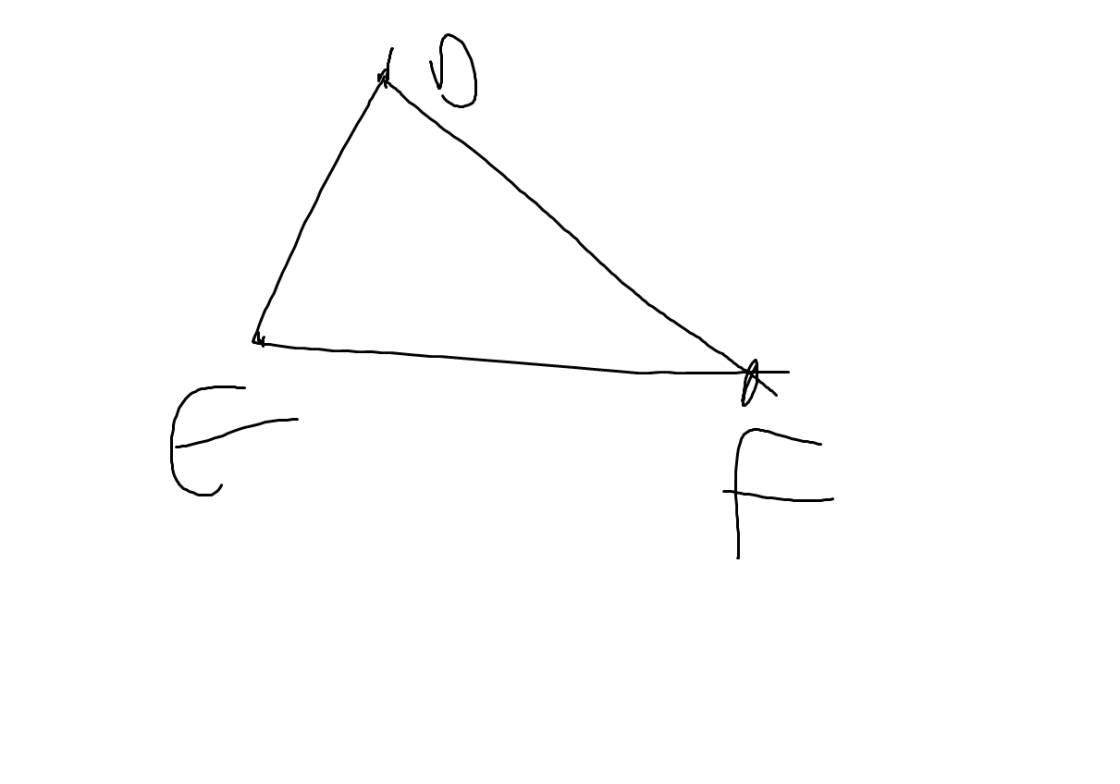
Xét ΔDEF có DE<DF<EF
mà \(\widehat{F};\widehat{E};\widehat{D}\) lần lượt là góc đối diện của các cạnh DE,DF,EF
nên \(\widehat{F}< \widehat{E}< \widehat{D}\)