Tính
K=(1-3/8)(1-3/15)....(1-3/399)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

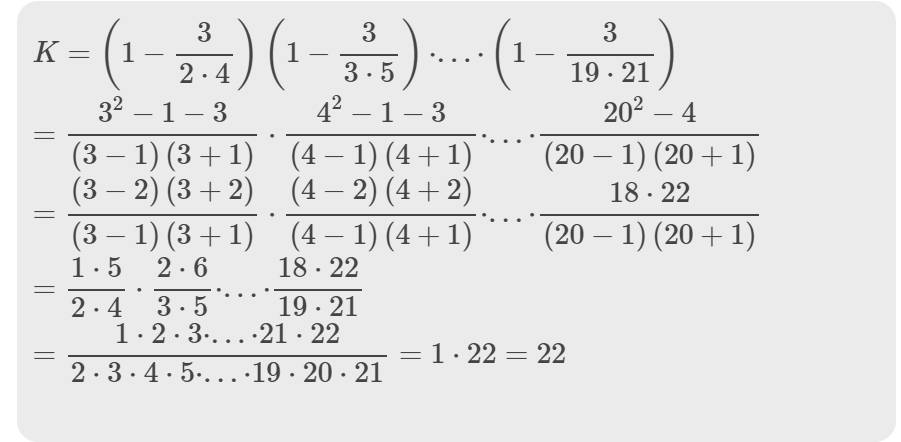

\(K=\left(1-\dfrac{3}{2\cdot4}\right)\left(1-\dfrac{3}{3\cdot5}\right)\cdot...\cdot\left(1-\dfrac{3}{19\cdot21}\right)\)
\(=\dfrac{3^2-1-3}{\left(3-1\right)\left(3+1\right)}\cdot\dfrac{4^2-1-3}{\left(4-1\right)\left(4+1\right)}\cdot...\cdot\dfrac{20^2-4}{\left(20-1\right)\left(20+1\right)}\)
\(=\dfrac{\left(3-2\right)\left(3+2\right)}{\left(3-1\right)\left(3+1\right)}\cdot\dfrac{\left(4-2\right)\left(4+2\right)}{\left(4-1\right)\left(4+1\right)}\cdot...\cdot\dfrac{18\cdot22}{\left(20-1\right)\left(20+1\right)}\)
\(=\dfrac{1\cdot5}{2\cdot4}\cdot\dfrac{2\cdot6}{3\cdot5}\cdot...\cdot\dfrac{18\cdot22}{19\cdot21}\)
\(=\dfrac{1\cdot2\cdot3\cdot...\cdot21\cdot22}{2\cdot3\cdot4\cdot5\cdot...\cdot19\cdot20\cdot21}=1\cdot22=22\)

\(=\frac{1}{2}\left(1-\frac{1}{399}\right)=\frac{1}{2}.\frac{1}{399}=\frac{1}{798}.\)


1+3-5-7+9+11-13-15+...-397-399
= 1 + (3-5-7+9) + (11-13-15+17)+...+ (397-399-401+403)+401-403
= 1+0+0+....+0+401-403
=1+401-403
=-1

bạn ơi , đây là cộng trừ các số lẻ đúng ko ?
nếu vậy thì tại sao lại có số 14 ở đây ?

\(4.B=\frac{4}{1.5}+\frac{4}{5.9}+\frac{4}{9.13}+...+\frac{4}{93.97}\)
\(4.B=1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+\frac{1}{9}-\frac{1}{13}+...+\frac{1}{93}-\frac{1}{97}\)
\(4.B=1-\frac{1}{97}\)
\(4.B=\frac{96}{97}\)
\(B=\frac{96}{97}:4\)
\(B=\frac{24}{97}\)

\(B=\frac{2}{15}+\frac{2}{35}+\frac{2}{63}+...+\frac{2}{399}\)
\(B=\frac{2}{3×5}+\frac{2}{5×7}+\frac{2}{7×9}+...+\frac{2}{19×21}\)
\(B=\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+\frac{1}{19}-\frac{1}{21}\)
\(B=\frac{1}{3}-\frac{1}{21}\)
\(B=\frac{2}{7}\)
A=\(\frac{1}{3}\)+\(\frac{1}{6}\)+\(\frac{1}{10}\)+\(\frac{1}{15}\)+...+\(\frac{1}{66}\)
A=\(\frac{1}{1\cdot3}\) +\(\frac{1}{2\cdot3}\) +\(\frac{1}{2\cdot5}\)+...+\(\frac{1}{6\cdot11}\)
A=\(\frac{1}{1}-\frac{1}{3}+\frac{1}{2}-\frac{1}{3}+\frac{1}{2}-\frac{1}{5}+...+\frac{1}{6}-\frac{1}{11}\)
A=\(\frac{1}{1}-\frac{1}{11}\)
=>A=\(\frac{10}{11}\)
B=\(\frac{2}{15}+\frac{2}{35}+\frac{2}{63}+...+\frac{2}{399}\)
2B=\(\frac{1}{3\cdot5}+\frac{1}{5\cdot7}+\frac{1}{7\cdot9}+...+\frac{1}{19\cdot21}\)
2B=\(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+...+\frac{1}{19}-\frac{1}{21}\)
2B=\(\frac{1}{3}-\frac{1}{21}\)
2B=\(\frac{2}{7}\)
B=\(\frac{2}{7}:2\)
=>B=\(\frac{1}{7}\)

3/15+3/35+...+3/399
Đặt S=3/15+3/35+...+3/399
=> S=3/3.5+3/5.7+..+3/19.21
=> S=(3/3.5+3/5.7+...+3/19.21).2
=> S=2.3/3.5+2.3/5.7+...+2.3/19.21
=> S=3.(2/3.5+2/5.7+...+2/19.21)
=> S=3.(1/3-1/5+1/5-1/7+...+1/19-1/21)
=> S=3.(1/3-1/21)
=> S=3.2/7
=> S=6/7
Vậy 3/15+3/35+...+3/399=6/7
\(\frac{3}{15}+\frac{3}{35}+\frac{3}{63}+...+\frac{3}{399}\)
\(=\frac{3}{3.5}+\frac{3}{5.7}+\frac{3}{7.9}+...+\frac{3}{399}\)
\(=\frac{3}{2}.\left(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+...+\frac{1}{19.21}\right)\)
\(=\frac{3}{2}.\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+...+\frac{1}{19}-\frac{1}{21}\right)\)
\(=\frac{3}{2}.\left(\frac{1}{3}-\frac{1}{21}\right)\)
\(=\frac{3}{2}.\frac{2}{7}\)
\(=\frac{3}{7}\)