K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
30 tháng 4 2022
Lời giải:
Vế trái luôn không âm (tính chất trị tuyệt đối)
$\Rightarrow -11x\geq 0$
$\Rightarrow x\leq 0$
Do đó: $x-\frac{1}{3}, x-\frac{1}{15},..., x-\frac{1}{399}<0$
PT trở thành:
$\frac{1}{3}-x+\frac{1}{15}-x+...+\frac{1}{399}-x=-11x$
$(\frac{1}{3}+\frac{1}{15}+...+\frac{1}{399})-10x=-11x$
$\frac{1}{1.3}+\frac{1}{3.5}+...+\frac{1}{19.21}=-x$
$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+..+\frac{1}{19}-\frac{1}{21})=-x$
$\frac{1}{2}(1-\frac{1}{21})=-x$
$\frac{10}{21}=-x$
$\Rightarrow x=\frac{-10}{21}$
AH
Akai Haruma
Giáo viên
30 tháng 4 2022
Lời giải:
Vế trái luôn không âm (tính chất trị tuyệt đối)
$\Rightarrow -11x\geq 0$
$\Rightarrow x\leq 0$
Do đó: $x-\frac{1}{3}, x-\frac{1}{15},..., x-\frac{1}{399}<0$
PT trở thành:
$\frac{1}{3}-x+\frac{1}{15}-x+...+\frac{1}{399}-x=-11x$
$(\frac{1}{3}+\frac{1}{15}+...+\frac{1}{399})-10x=-11x$
$\frac{1}{1.3}+\frac{1}{3.5}+...+\frac{1}{19.21}=-x$
$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+..+\frac{1}{19}-\frac{1}{21})=-x$
$\frac{1}{2}(1-\frac{1}{21})=-x$
$\frac{10}{21}=-x$
$\Rightarrow x=\frac{-10}{21}$
PH
16 tháng 5 2022
a.-1,75-(-\(\dfrac{1}{9}\)-2\(\dfrac{1}{8}\))
-1,75-\(\dfrac{1}{9}+\dfrac{17}{8}\)
\(-\dfrac{7}{4}-\dfrac{1}{9}+\dfrac{17}{8}\)
\(\dfrac{-126}{72}-\dfrac{8}{72}+\dfrac{153}{72}\)
=\(\dfrac{19}{72}\)
PH
16 tháng 5 2022
b.\(\dfrac{-1}{12}-\left(2\dfrac{5}{8}-\dfrac{1}{3}\right)\)
\(\dfrac{-1}{12}-\left(\dfrac{21}{8}-\dfrac{1}{3}\right)\)
\(\dfrac{-1}{12}-\dfrac{21}{8}+\dfrac{1}{3}\)
\(\dfrac{-2}{24}-\dfrac{63}{24}+\dfrac{64}{24}\)
=\(\dfrac{-1}{24}\)
24 tháng 7 2020
Bài làm:
a) \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
\(=\left[\left(x+1\right)\left(x+4\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
Đặt \(x^2+5x+5=t\)\(\Rightarrow\left(t-1\right)\left(t+1\right)+1=t^2-1+1=t^2\)
\(=\left(x^2+5x+5\right)^2\)
b) Tương tự như a phân tích và đặt ra được: \(t^2-1-24=t^2-25=\left(t-5\right)\left(t+5\right)\)
\(=\left(x^2+5x\right)\left(x^2+5x+10\right)=x\left(x+5\right)\left(x^2+5x+10\right)\)
c) \(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+15\)
\(=\left[\left(x+1\right)\left(x+7\right)\right]\left[\left(x+3\right)\left(x+5\right)\right]+15\)
\(=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15\)
Đặt \(x^2+8x+11=t\)\(\Rightarrow\left(t-4\right)\left(t+4\right)+15=t^2-16+15=t^2-1\)
\(=\left(t-1\right)\left(t+1\right)=\left(x^2+8x+10\right)\left(x^2+8x+12\right)\)
\(=\left(x^2+8x+10\right)\left(x+2\right)\left(x+6\right)\)
d) \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left[\left(x+2\right)\left(x+5\right)\right]\left[\left(x+3\right)\left(x+4\right)\right]-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
Đặt \(x^2+7x+11=t\)\(\Rightarrow\left(t-1\right)\left(t+1\right)-24=t^2-1-24=t^2-25\)
\(=\left(t-5\right)\left(t+5\right)=\left(x^2+7x+6\right)\left(x^2+7x+16\right)\)
\(=\left(x+1\right)\left(x+6\right)\left(x^2+7x+16\right)\)
24 tháng 7 2020
Làm mẫu cho 1 vd:
a, (x+1)(x+2)(x+3)(x+4)+1
\(=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)(1)
Đặt \(y=x^2+5x+5\)
Khi đó ::
(1) = \(\left(y-1\right)\left(y+1\right)+1\)
\(=y^2-1+1=y^2\)
Thay vào ta được: \(\left(x^2+5x+5\right)^2\)
21 tháng 7 2023
1: x=3/4-1/2=3/4-2/4=1/4
2: x-1/5=2/11
=>x=2/11+1/5=21/55
3: x-5/6=16/42-8/56
=>x-5/6=8/21-4/28=5/21
=>x=5/21+5/6=15/14
4: x/5=5/6-19/30
=>x/5=25/30-19/30=6/30=1/5
=>x=1
5: =>|x|=1/3+1/4=7/12
=>x=7/12 hoặc x=-7/12
6: x=-1/2+3/4
=>x=3/4-1/2=1/4
11: x-(-6/12)=9/48
=>x+1/2=3/16
=>x=3/16-1/2=-5/16
21 tháng 7 2023
1)x= 1/4
2)x= 2/11+ 1/5
x= 21/55
3)x - 5/6 = 5/21
x = 5/21+5/6
x = 15/14
4)x/5 = 5/6 + -19/30
x:5 = 1/5
x = 1/5.5
x = 1
5) |x| - 1/4 = 6/18
|x| = 6/18 - 1/4
|x| =7/12
⇒x= 7/12 hoặc -7/12
6)x = -1/2 +3/4
x= 1/4
7) x/15 = 3/5 + -2/3
x:15 = -1/15
x = -1/15. 15
x = -1
8)11/8 + 13/6 = 85/x
85/24 = 85/x
⇒ x = 24
9) x - 7/8 = 13/12
x = 13/12 + 7/8
x = 47/24
10)x - -6/15 = 4/27
x = 4/27 + (-6/15)
x = -34/135
11) -(-6/12)+x = 9/48
x= 9/48 - 6/12
x = -5/16
12) x - 4/6 = 5/25 + -7/15
x -4/6 = -4/15
x = -4/15 + 4/6
x = 2/5
DS
1
1 tháng 7 2023
`1/2-(1/3+3/4)<=x<=1/24-(1/8-1/3)`
`<=>6/12-4/12-9/12<=x<=1/24-3/24+8/24`
`<=>-7/12<=x<=1/4`
`<=>-14/24<=x<=3/12`
`=>-14<=x<=3`
`=>x\in{-14;-13;-12;...;3}` do `x\inZZ`
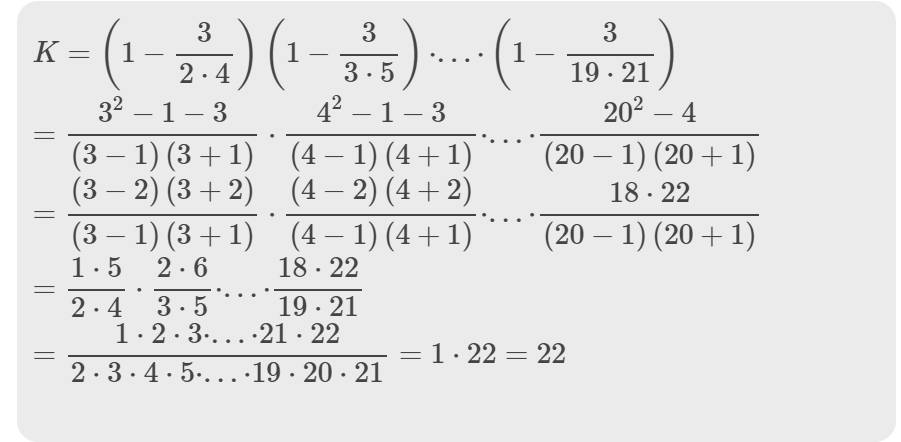
\(K=\left(1-\dfrac{3}{2\cdot4}\right)\left(1-\dfrac{3}{3\cdot5}\right)\cdot...\cdot\left(1-\dfrac{3}{19\cdot21}\right)\)
\(=\dfrac{3^2-1-3}{\left(3-1\right)\left(3+1\right)}\cdot\dfrac{4^2-1-3}{\left(4-1\right)\left(4+1\right)}\cdot...\cdot\dfrac{20^2-4}{\left(20-1\right)\left(20+1\right)}\)
\(=\dfrac{\left(3-2\right)\left(3+2\right)}{\left(3-1\right)\left(3+1\right)}\cdot\dfrac{\left(4-2\right)\left(4+2\right)}{\left(4-1\right)\left(4+1\right)}\cdot...\cdot\dfrac{18\cdot22}{\left(20-1\right)\left(20+1\right)}\)
\(=\dfrac{1\cdot5}{2\cdot4}\cdot\dfrac{2\cdot6}{3\cdot5}\cdot...\cdot\dfrac{18\cdot22}{19\cdot21}\)
\(=\dfrac{1\cdot2\cdot3\cdot...\cdot21\cdot22}{2\cdot3\cdot4\cdot5\cdot...\cdot19\cdot20\cdot21}=1\cdot22=22\)