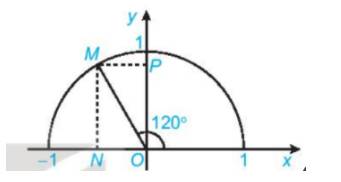
Tìm các giá trị lượng giác của góc \({120^o}\) (H.3.4)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
Lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\), H là hình chiếu vuông góc của M trên Oy.
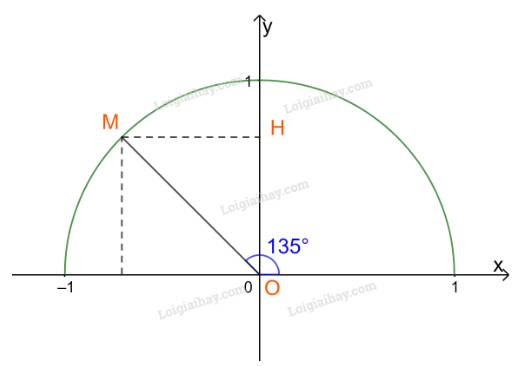
Ta có: \(\widehat {MOy} = {135^o} - {90^o} = {45^o}\).
Tam giác OMH vuông cân tại H nên \(OH = MH = \frac{{OM}}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}.\)
Vậy tọa độ điểm M là \(\left( { - \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right).\)
Vậy theo định nghĩa ta có:
\(\begin{array}{l}\;\sin {135^o} = \frac{{\sqrt 2 }}{2};\;\;\cos {135^o} = - \frac{{\sqrt 2 }}{2};\\\;\tan {135^o} = - 1;\;\;\cot {135^o} = - 1.\end{array}\)
Chú ý
Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({135^o}\)
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính \(\sin {135^o}\), bấm phím: sin 1 3 5 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 2 }}{2}\)
Tính \(\cos {135^o}\),bấm phím: cos 1 3 5 \(^o\)’’’ = ta được kết quả là \(\frac{{ - \sqrt 2 }}{2}\)
Tính \(\tan {135^o}\), bấm phím: tan 1 3 5 \(^o\)’’’ = ta được kết quả là \( - 1\)
(Để tính \(\cot {135^o}\), ta tính \(1:\tan {135^o}\))

a) \(\left\{{}\begin{matrix}sin120^o=\dfrac{\sqrt{3}}{2}\\cos120^o=-\dfrac{1}{2}\\tan120^o=-\sqrt{3}\\cot120^o=-\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}sin150^o=\dfrac{1}{2}\\cos150^o=-\dfrac{\sqrt{3}}{2}\\tan150^o=-\dfrac{\sqrt{3}}{3}\\cot150^o=-\sqrt{3}\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}sin180^o=0\\cos180^o=-1\\tan180^o=0\\cot180^o\left(\varnothing\right)\end{matrix}\right.\)

\(\begin{array}{l}\sin {120^o} = \sin \;({180^o} - {60^o}) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\cos {150^o} = - \cos \;({180^o} - {30^o}) = - \cos {30^o} = - \frac{{\sqrt 3 }}{2};\\\cot {135^o} = - \cot \;({180^o} - {45^o}) = - \cot {45^o} = - 1.\end{array}\)

\(\sin \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\cos \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\tan \left( {45^\circ } \right) = \frac{1}{2};\,\,\cot \left( {45^\circ } \right) = 2\)

Các giá trị lượng giác của góc 120o là:
sin 120º = sin (180º – 60º) = sin 60º = √3/2.
cos 120º = cos(180º – 60º) = –cos 60º = –1/2
tan 120º = sin 120º / cos 120º = –√3
cot 120º = cos 120º / sin 120º = –1/√3
Các giá trị lượng giác của góc 150º là:
sin 150º = sin ( 180º – 30º ) = sin 30º = 1/2
cos 150º = –cos ( 180º – 30º ) = –cos 30º = (–√3)/2
tan 150º = sin 150º / cos 150º = –1/√3
cot 150º = cos 150º / sin 150º = –√3.

Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.


a) Do MN song song với Ox nên \(\alpha = \widehat {OMN} = \widehat {ONM} = \widehat {NOx'}\)
Mà \(\widehat {xON} = {180^o} - \widehat {NOx'} = {180^o} - \alpha \)
\( \Rightarrow \widehat {xON} = {180^o} - \alpha \)
b) Dễ thấy: Điểm N đối xứng với M qua trục Oy
\( \Rightarrow N( - {x_0};{y_0})\)
Lại có: điểm N biểu diễn góc \({180^o} - \alpha \)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = {y_N} = {y_0}\\\cos ({180^o} - \alpha ) = {x_N} = - {x_0}\end{array} \right.\);
Mà: \(\sin \alpha = {y_0};\;\cos \alpha = {x_0}\)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = \sin \alpha \;\\\cos ({180^o} - \alpha ) = - \cos \alpha \end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\tan ({180^o} - \alpha ) = - \tan \alpha \;\\\cot ({180^o} - \alpha ) = - \cot \alpha \end{array} \right.\)
Tham khảo:
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {120^o}\)
Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Vì \(\widehat {xOM} = {120^o} > {90^o}\) nên M nằm bên trái trục tung.
Khi đó:\(\;\cos {120^o} = - \,\;\overline {ON} ,\;\;\sin {120^o} = \overline {OP} \)
Vì \(\widehat {xOM} = {120^o}\) nên \(\widehat {NOM} = {180^o} - {120^o} = {60^o}\) và \(\widehat {POM} = {120^o} - {90^o} = {30^o}\)
Vậy các tam giác \(\Delta MON\) và \(\Delta MOP\) vuông tại N, p và có một góc bằng \({30^o}\)
\( \Rightarrow ON = MP = \frac{1}{2}OM = \frac{1}{2}\)(Trong tam giác vuông, cạnh đối diện góc \({30^o}\) bằng một nửa cạnh huyền)
Và \(OP = MN = \sqrt {O{M^2} - O{N^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)
Vậy điểm M có tọa độ là \(\left( { - \frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)\).
Và \(\cos {120^o} = - \frac{1}{2};\;\;\;\sin {120^o} = \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l}\; \Rightarrow \;\tan {120^o} = \frac{{\sin {{120}^o}}}{{\cos {{120}^o}}} = \frac{{\sqrt 3 }}{2}:\left( { - \frac{1}{2}} \right) = - \sqrt 3 ;\\\cot {120^o} = \frac{{\cos {{120}^o}}}{{\sin {{120}^o}}} = \left( { - \frac{1}{2}} \right):\frac{{\sqrt 3 }}{2} = \frac{{ - 1}}{{\sqrt 3 }} = - \frac{{\sqrt 3 }}{3}.\end{array}\)
Chú ý
Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({120^o}\)
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính \(\sin {120^o}\), bấm phím: sin 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 3 }}{2}\)
Tính \(\cos {120^o}\),bấm phím: cos 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{ - 1}}{2}\)
Tính \(\tan {120^o}\), bấm phím: tan 1 2 0 \(^o\)’’’ = ta được kết quả là \( - \sqrt 3 \)
( Để tính \(\cot {120^o}\), ta tính \(1:\tan {120^o}\))