BT7: viết các biểu thức sau thành đa thức 1, (2x-3)^3 2, (a+3b)^3 3, (xy-1)^3 4, (2ab+3)^3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

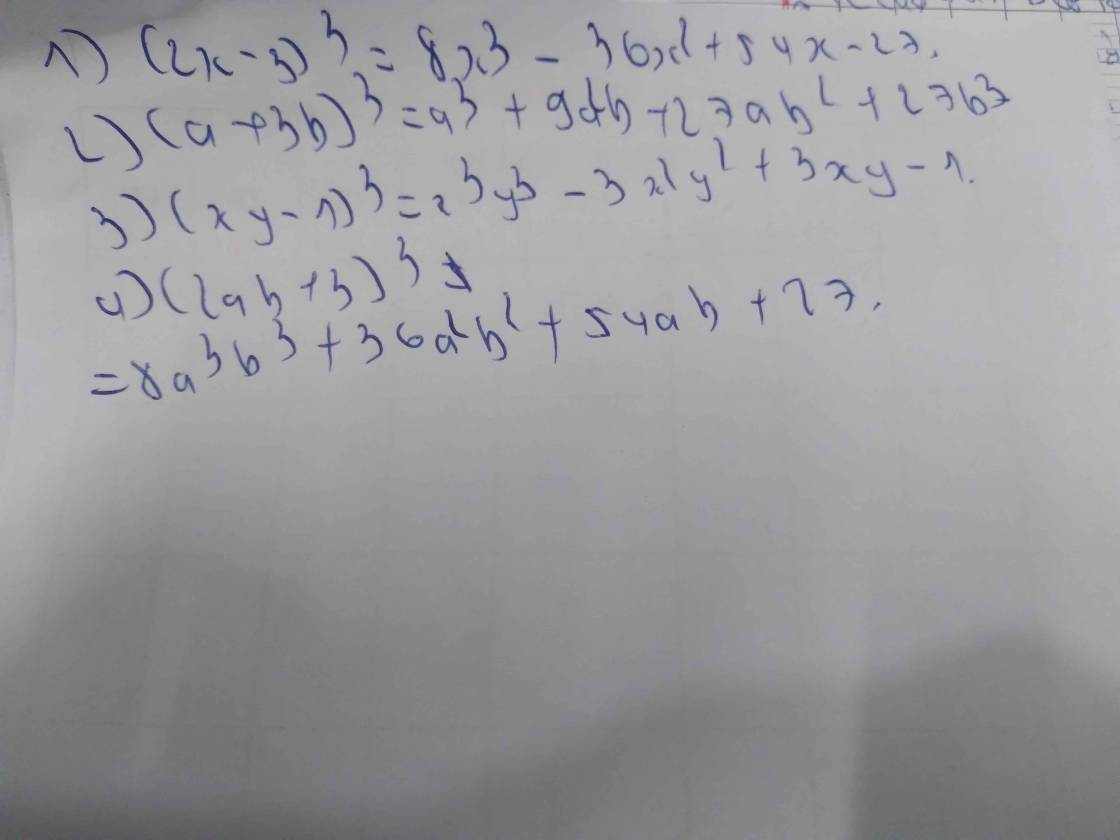

`a, (2x-3)^3 = 8x^3 - 36x^2 + 54x - 27`
`b, (a+3b)^3 = a^3 + 9a^2b + 27ab^2 + 27b^3`
`c, (xy-1)^3 = x^3y^3 - 3x^2y^2 + 3xy -1`

Câu 1:
-2x²y + xy + 1 = -2x²y + (xy + 1)
Vậy -2x²y + xy + 1 được viết thành tổng của hai đa thức: -2x²y và xy + 1
Câu 2:
x²y² + 2xy - 3 = x²y² + (2xy - 3)
Vậy x²y² + 2xy - 3 được viết thành tổng của hai đa thức: x²y² và 2xy - 3
Câu 3:
-2x²y + xy + 1 = (xy + 1) - 2x²y
Vậy -2x²y + xy + 1 được viết thành hiệu của hai đa thức: xy + 1 và 2x²y
Câu 4:
x²y² - 2xy + 3 = (x²y² + 3) - 2xy
Vậy x²y² - 2xy + 3 được viết thành hiệu của hai đa thức: x²y² + 3 và 2xy

1)
x2-y2-2x+2y
=(x-y)(x+y)-2(x-y)
=(x-y)(x+y-2)
2)
2x+2y-x2-xy
=2(x+y)-x(x+y)
=(2-x)(x+y)
3)
3a2-6ab+3b2-12c2
=3(a2-2ab+b2)-3(4c2)
=3(a-b)2-3(4c2)
=3[(a-b)2-4c2 ]
=3(a-b-2c)(a-b+2c)
4)
x2-25+y2+2xy
=(x+y)2-25
=(x+y-5)(x+y+5)
1) x^2 - y^2 - 2x + 2y= ( x^2 - y^2) - ( 2x + 2y) = (x-y -2 ) (x+y)
2) 2x + 2y - x^2 - xy = 2 (x+y) - x(x+y) = (2-x)(x+y)
4) x^2 - 25 + y^2 +2xy = x^2 + 2xy + y^2 - 25 = (x+y)^2 - 5^2 = (x+y-5)(x+y+5)
5) a^2 + 2ab +b^2-ac-bc= (a+b)^2- ac + bc = (a+b)^2 - c(a+b) = (a+b)(a+b-c)
6) x^2 - 2x - 4y^2 - 4y = (x^2 - 4y^2) - (2x+4y) = (x - 2y)(x+2y) - 2 (x+2y) = (x-2y-2)(x+2y)
7) x^2y - x^3 - 9y + 9x = x^2 (y-x) - 9(y-x) = (x^2 - 9)(y-x)= (x^2 - 3^2)(y-x) = (x-3)(x+3)(y-x)
- Xl câu 3 , 8 t hk biết lm

\(\left(2x+1\right)^2-2\left(2x+1\right)\left(3-x\right)+\left(x-3\right)^2\)
\(=\left(2x+1\right)^2+2\left(2x-1\right)\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(2x+1+x-3\right)^2\)
\(=\left(3x-2\right)^2\)
------------------------------------
\(a^3+3a^2-6a-8\)
\(=a^3+4a^2-a^2-4a-2a-8\)
\(=\left(a^3+4a^2\right)-\left(a^2+4a\right)-\left(2a+8\right)\)
\(=a^2\left(a+4\right)-a\left(a+4\right)-2\left(a+4\right)\)
\(=\left(a+4\right)\left(a^2-a-2\right)\)
\(=\left(a+4\right)\left(a^2-2a+a-2\right)\)
\(=\left(a+4\right)\left[\left(a^2-2a\right)+\left(a-2\right)\right]\)
\(=\left(a+4\right)\left[a\left(a-2\right)+\left(a-2\right)\right]\)
\(=\left(a+4\right)\left(a-2\right)\left(a+1\right)\)
---------------------------------
\(2x^2-5x+2\)
\(=2x^2-4x-x+2\)
\(=\left(2x^2-4x\right)-\left(x-2\right)\)
\(=2x\left(x-2\right)-\left(x-2\right)\)
\(=\left(x-2\right)\left(2x-1\right)\)
-----------------------------------------
\(x^2-2x-4y^2-4y\)
\(=\left(x^2-4y^2\right)-\left(2x-4y\right)\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x-2y\right)\)
\(=\left(x-2y\right)\left(x+2y-2\right)\)
-------------------------------------
\(a^2-1+4b-4b^2\)
\(=a^2-\left(1-4b+4b^2\right)\)
\(=a^2-\left(1-2b\right)^2\)
\(=\left(a-1+2b\right)\left(a+1-2b\right)\)
----------------------------------------
\(a^4+6a^2b+9b^2-1\)
\(=\left(a^4+6a^2b+9b^2\right)-1\)
\(=\left(a^2+3b\right)^2-1\)
\(=\left(a^2+3b-1\right)\left(a^2+3b+1\right)\)
---------------------------------
\(2x^3+16y^3\)
\(=2\left(x^3+8y^3\right)\)
\(=2\left(x+2y\right)\left(x^2-2xy+4y^2\right)\)
Lần sau ghi đề tách riêng từng câu ra nhé em. Ghi dính chùm vậy khó nhìn lắm. Sẽ ít ai giải cho em

1) \(2\left(x-1\right)^3-\left(x-1\right)=\left(x-1\right)\left(2\left(x-1\right)^2-1\right)\)
2) \(y\left(x-2y\right)^2+xy^2\left(2y-x\right)=\left(2y-x\right)\left(2\left(2y-x\right)+1\right)=\left(2y-x\right)\left(4y-2x+1\right)\)
3) \(xy\left(x+y\right)-x-y=xy\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(xy-1\right)\) (xem lại đề sửa -2x thành -x mới đúng)
4) \(xy\left(x-3y\right)-2x+6y=xy\left(x-3y\right)-2\left(x-3y\right)=\left(x-3y\right)\left(xy-2\right)\)

Các đơn thức là:
\(-3;2z;-10x^2yz;\dfrac{4}{xy}\)
Các đa thức là:
\(\dfrac{1}{3}xy+1;5x-\dfrac{z}{2};1+\dfrac{1}{y}\)

B) Ta có: 2x-2y-x2+2xy-y2
⇔ 2(x-y)-(x2-2xy+y2)
⇔ 2(x-y)-(x-y)2
⇔ (x-y)(2-x+y)
Đúng thì tick nhé

\(3,\)Nhẩm nghiệm của đa thức trên ta đc : -1
Ta có lược đồ sau :
| 1 | 1 | -4 | -4 | |
| -1 | 1 | 0 | -4 | 0 |
Phân tích thành nhân tử ta có :\(\left(x+1\right)\left(x^2-4\right)\)