tìm khoảng đồng biến nghịch biến của các hàm số
a) y = \(x^3\) - \(3x^2\) +1
b) y = \(-x^3\) + \(3x\) - 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tròi oi a viết chữ xấu wá đi à, đọc bài của a mà đau mắt wá

a: y'=-4x^3+8*2x
=-4x^3+16x
y'>0 khi -4x^3+16x>0
=>-4x(x^2-4)>0
=>x(x^2-4)<0
=>x<-2; 0<x<2
Vậy: Khi x<-2 hoặc 0<x<2 thì hàm số đồng biến
y'<0 khi -4x^3+16x<0
=>-2<x<0; x>2
Vậy: Khi -2<x<0 hoặc x>2 thì hàm số nghịch biến
b: y'=4x^3
y'>0 khi x>0
=>Khi x>0 thì hàm số đồng biến
y'<0 khi 4x^3<0
=>x<0
=>Khi x<0 thì hàm số nghịch biến

a: \(y'< 0\)
=>\(\left(x-3\right)^3\cdot\left(x-1\right)^{22}\cdot\left(-3x-6\right)^7< 0\)
=>\(\left(x-3\right)\left(-3x-6\right)< 0\)
=>\(\left(x+2\right)\left(x-3\right)>0\)
=>\(\left[{}\begin{matrix}x>3\\x< -2\end{matrix}\right.\)
y'>0
=>\(\left(x+2\right)\left(x-3\right)< 0\)
=>\(-2< x< 3\)
y'=0
=>\(\left[{}\begin{matrix}x-3=0\\x-1=0\\-3x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\\x=-2\end{matrix}\right.\)
Ta có bảng xét dấu sau:
| x | \(-\infty\) -2 1 3 +\(\infty\) |
| y' | - 0 + 0 + 0 - |
Vậy: Hàm số đồng biến trên các khoảng \(\left(-2;1\right);\left(1;3\right)\)
Hàm số nghịch biến trên các khoảng \(\left(-\infty;-2\right);\left(3;+\infty\right)\)
b: y'<0
=>\(\left(4x-3\right)^3\cdot\left(x^2-1\right)^{21}\left(3x-9\right)^7< 0\)
=>\(\left(4x-3\right)\left(3x-9\right)\left(x^2-1\right)< 0\)
=>\(\left(4x-3\right)\left(x-3\right)\left(x^2-1\right)< 0\)
TH1: \(\left\{{}\begin{matrix}\left(4x-3\right)\left(x-3\right)>0\\x^2-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>3\\x< \dfrac{3}{4}\end{matrix}\right.\\-1< x< 1\end{matrix}\right.\Leftrightarrow-1< x< \dfrac{3}{4}\)
TH2: \(\left\{{}\begin{matrix}\left(4x-3\right)\left(x-3\right)< 0\\x^2-1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{4}< x< 3\\\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow1< x< 3\)
y'>0
=>\(\left(4x-3\right)\left(x-3\right)\left(x^2-1\right)>0\)
TH1: \(\left\{{}\begin{matrix}\left(4x-3\right)\left(x-3\right)>0\\x^2-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>3\\x< \dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>3\\x< -1\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}\left(4x-3\right)\left(x-3\right)< 0\\x^2-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{4}< x< 3\\-1< x< 1\end{matrix}\right.\Leftrightarrow\dfrac{3}{4}< x< 1\)
Ta sẽ có bảng xét dấu sau đây:
| x | \(-\infty\) -1 3/4 1 3 +\(\infty\) |
| y' | + 0 - 0 + 0 - 0 + |
Vậy: Hàm số đồng biến trên các khoảng \(\left(-\infty;-1\right);\left(\dfrac{3}{4};1\right);\left(3;+\infty\right)\)
Hàm số nghịch biến trên các khoảng \(\left(-1;\dfrac{3}{4}\right);\left(1;3\right)\)

Bài 1:
Để hàm số y=(2-m)x-2 là hàm số bậc nhất thì 2-m<>0
=>m<>2
a=2-m
b=-2
Bài 2:
a: Để hàm số y=(m-5)x+1 đồng biến trên R thì m-5>0
=>m>5
b: Để hàm số y=(m-5)x+1 nghịch biến trên R thì m-5<0
=>m<5
Bài 3:
a: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}3-m=2\\2\ne m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=1\)
b: Để (d1) cắt (d2) thì \(3-m\ne2\)
=>\(m\ne1\)
c: Để (d1) cắt (d2) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}3-m\ne2\\m=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\m=2\end{matrix}\right.\)
=>m=2

a: \(y=-x^3+\left(m+2\right)x^2-3x\)
=>\(y'=-3x^2+2\left(m+2\right)x-3\)
=>\(y'=-3x^2+\left(2m+4\right)\cdot x-3\)
Để hàm số nghịch biến trên R thì \(y'< =0\forall x\)
=>\(\left\{{}\begin{matrix}\left(2m+4\right)^2-4\cdot\left(-3\right)\left(-3\right)< =0\\-3< 0\end{matrix}\right.\)
=>\(4m^2+16m+16-4\cdot9< =0\)
=>\(4m^2+16m-20< =0\)
=>\(m^2+4m-5< =0\)
=>\(\left(m+5\right)\left(m-1\right)< =0\)
TH1: \(\left\{{}\begin{matrix}m+5>=0\\m-1< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>=-5\\m< =1\end{matrix}\right.\)
=>-5<=m<=1
TH2: \(\left\{{}\begin{matrix}m+5< =0\\m-1>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>=1\\m< =-5\end{matrix}\right.\)
=>\(m\in\varnothing\)
b: \(y=x^3-3x^2+\left(1-m\right)x\)
=>\(y'=3x^2-3\cdot2x+1-m\)
=>\(y'=3x^2-6x+1-m\)
Để hàm số đồng biến trên R thì \(y'>=0\forall x\)
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3>0\\\left(-6\right)^2-4\cdot3\left(1-m\right)>=0\end{matrix}\right.\)
=>\(36-12\left(1-m\right)>=0\)
=>\(36-12+12m>=0\)
=>12m+24>=0
=>m+2>=0
=>m>=-2

a: \(y=-x^3-3x^2+\left(5-m\right)x\)
=>\(y'=-3x^2-3\cdot2x+5-m\)
=>\(y'=-3x^2-6x+5-m\)
Để hàm số nghịch biến trên R thì \(y'< =0\forall x\)
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(-6\right)^2-4\cdot\left(-3\right)\left(5-m\right)< =0\\-3< 0\end{matrix}\right.\)
=>\(36+12\left(5-m\right)< =0\)
=>\(36+60-12m< =0\)
=>\(-12m+96< =0\)
=>-12m<=-96
=>m>=8
b: \(y=x^3+\left(2m-2\right)\cdot x^2+mx\)
=>\(y'=3x^2+2\left(2m-2\right)\cdot x+m\)
=>\(y'=3x^2+\left(4m-4\right)x+m\)
Để hàm số đồng biến trên R thì y'>=0 với mọi x
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3>0\\\left(4m-4\right)^2-4\cdot3\cdot m< =0\end{matrix}\right.\)
=>\(16m^2-32m+16-12m< =0\)
=>\(16m^2-44m+16< =0\)
=>\(4m^2-11m+4< =0\)
=>\(\dfrac{11-\sqrt{57}}{8}< =m< =\dfrac{11+\sqrt{57}}{8}\)

TXĐ: R \ {2}
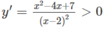
(do x 2 − 4x + 7 x 2 − 4x + 7 có ∆ ' = - 3 < 0)
Vậy hàm số đã cho đồng biến trên các khoảng (− ∞ ;2),(2;+ ∞ )
a: y'=3x^2-3*2x=3x^2-6x=3x(x-2)
y'>0 khi x(x-2)>0
=>x>2 hoặc x<0
=>Khi x>2 hoặc x<0 thì hàm số đồng biến
y'<0 khi x(x-2)<0
=>0<x<2
=>Khi 0<x<2 thì hàm số nghịch biến
b: y'=-3x^2+3
y'>0 khi -3x^2+3>0
=>-3x^2>-3
=>x^2<1
=>-1<x<1
Khi -1<x<1 thì hàm số đồng biến
y'<0 khi x^2>1
=>x>1 hoặc x<-1
Vậy: Khi x>1 hoặc x<-1 thì hàm số nghịch biến