m.n giúp em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.frightened
2.frightening
3.depressing
4.depressed
5.excited
6.interesting
7.thrilling
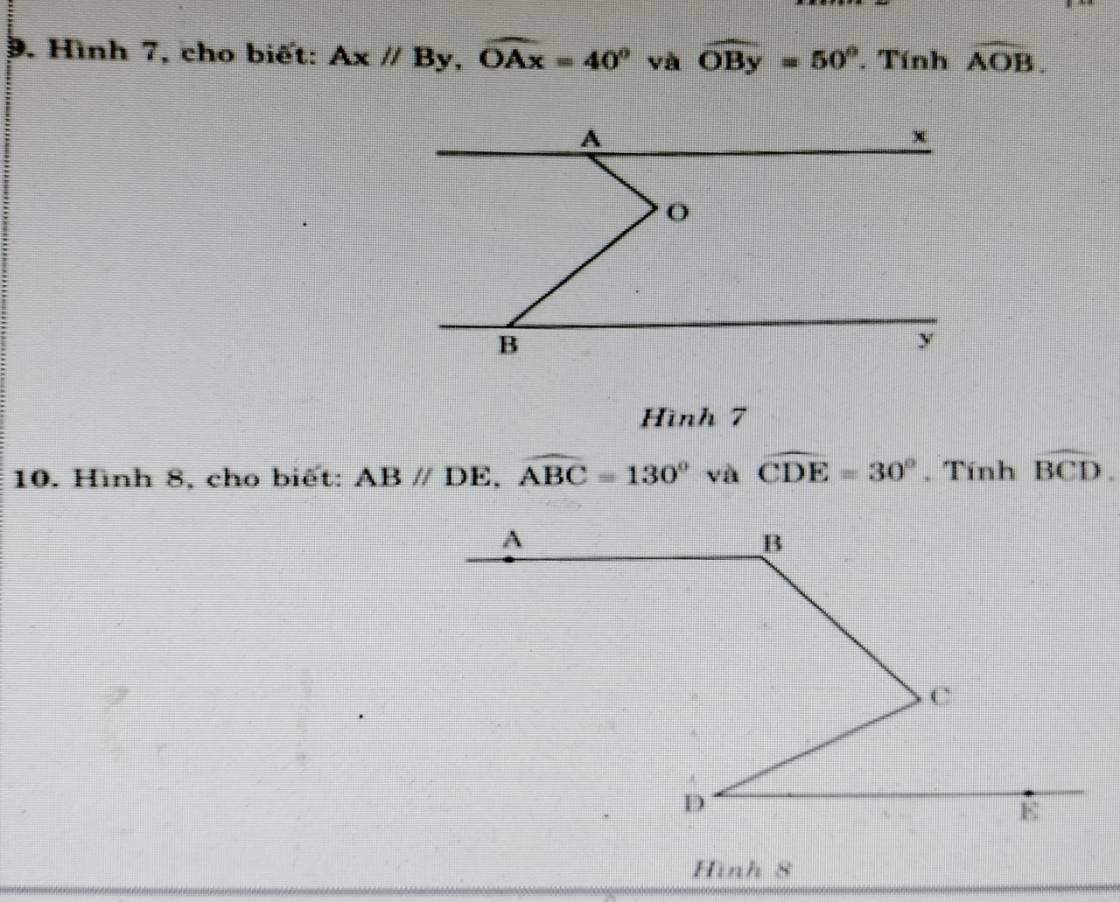
8.embarrassed
9.exhausted
10.boring
frightened
frightening
depressing
depressed
excited
interesting
thrilling
embarrassed
exhausted
boring

Which do they prefer, a play or a film?

Bài 9
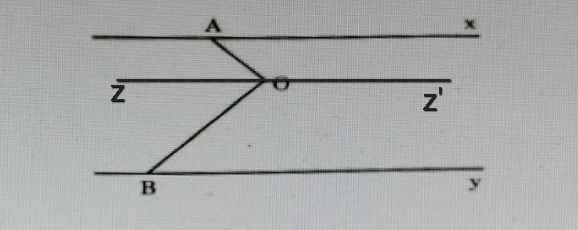
Qua O vẽ đường thẳng zz' // Ax // By
Do Ax // zz'
⇒ ∠AOz = ∠OAx = 40⁰
Do By // zz'
⇒ ∠zOB = ∠OBy = 50⁰ (so le trong)
⇒ ∠AOB = ∠AOz + ∠zOB
= 40⁰ + 50⁰
= 90⁰
Bài 10
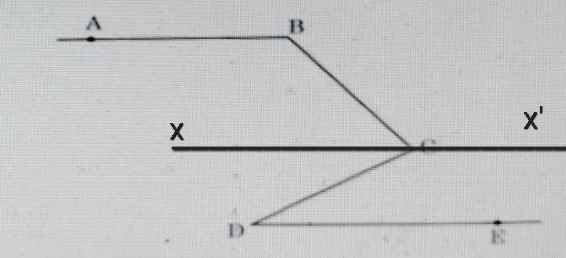 Qua C vẽ đường thẳng xx' // AB // DE
Qua C vẽ đường thẳng xx' // AB // DE
Do AB // xx'
⇒ ∠ABC = ∠BCx' = 130⁰ (so le trong)
Ta có:
∠BCx + ∠BCx' = 180⁰ (kề bù)
⇒ ∠BCx = 180⁰ - ∠BCx'
= 180⁰ - 130⁰
= 50⁰
Do DE // xx'
⇒ ∠xCD = ∠CDE = 30⁰ (so le trong)
⇒ ∠BCD = ∠BCx + ∠xCD
= 50⁰ + 30⁰
= 80⁰


dấu hiệu chia hết cho 6 là: số đó phải chia hết cho cả 2 và 3.
tick nha!

3:cây cao su :cây công ngiệp
4,cây tam thất:cây làm thuốc
5,cây phong lan:cây cảnh
6,cây xoài:cây ăn quả, cây lấy gỗ
tick nếu đúng nha

bn nhớ tick cho mình nha
7a
bn ko chụp câu 8
9a
10c
11b
12d
13a


 giup em voi mn ko can ve hinh dau de em tu ve cung dc a
giup em voi mn ko can ve hinh dau de em tu ve cung dc a




 mn giup mk cau nay voi a
mn giup mk cau nay voi a mn giup mk lm bai nay voi a
mn giup mk lm bai nay voi a
Bài 1. a) Do \(\Delta ABC\) cân tại A (giả thiết) nên \(AB=AC\) và \(\hat{B}=\hat{C}=\dfrac{180^o-\hat{A}}{2}\)
Theo đề bài, \(BD=CE\)
\(\Rightarrow AB-BD=AC-CE\Leftrightarrow AD=AE\).
Suy ra \(\Delta ADE\) cân tại A \(\Rightarrow\hat{D}=\hat{E}=\dfrac{180^o-\hat{A}}{2}\)
Suy ra được : \(\hat{B}=\hat{D}\). Mà hai góc này ở vị trí đồng vị nên \(DE\left|\right|BC\) (điều phải chứng minh).
b) Xét \(\Delta ABE,\Delta ACD\) có : \(\left\{{}\begin{matrix}\hat{A}\text{ chung}\\AD=AE\left(cmt\right)\\AB=AC\left(gt\right)\end{matrix}\right.\Rightarrow\Delta ABE=\Delta ADE\left(c.g.c\right)\)
c) Do \(\Delta ABE=\Delta ACD\left(cmt\right)\) nên \(\hat{DBI}=\hat{ECI}\) (hai góc tương ứng)
Xét các tam giác BID, CIE có : \(\left\{{}\begin{matrix}\hat{DBI}+\hat{DIB}+\hat{BDI}=180^o\\\hat{ECI}+\hat{EIC}+\hat{CIE}=180^o\\\hat{DIB}=\hat{EIC}\left(\text{đối đỉnh}\right);\hat{DBI}=\hat{ECI}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\hat{BDI}=\hat{CIE}\).
Lại xét \(\Delta BID,\Delta CIE\) có : \(\left\{{}\begin{matrix}\hat{BDI}=\hat{CIE}\left(cmt\right)\\BD=CE\left(gt\right)\\\hat{DBI}=\hat{ECI}\left(cmt\right)\end{matrix}\right.\Rightarrow\Delta BID=\Delta CIE\left(g.c.g\right)\) (điều phải chứng minh).
d) Do \(\Delta BID=\Delta CIE\left(cmt\right)\Rightarrow IB=IC\) (hai cạnh tương ứng).
Xét \(\Delta AIB,\Delta AIC\) có : \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\hat{ABI}=\hat{ACI}\left(cmt\right)\\IB=IC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AIB=\Delta AIC\left(c.g.c\right)\Rightarrow\hat{AIB}=\hat{AIC}\)
⇒ \(AI\) là phân giác của \(\hat{BAC}\) (điều phải chứng minh).
e) Gọi \(H\) là giao điểm của \(AI\) và \(BC\).
Xét \(\Delta AHB,\Delta AHC:\) \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\hat{IAB}=\hat{IAC}\left(cmt\right)\\AH\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.g.c\right)\Rightarrow\hat{AHB}=\hat{AHC}\).
Mà : \(\hat{AHB}+\hat{AHC}=180^o\) (hai góc kề bù)
\(\Rightarrow\hat{AHB}=\hat{AHC}=\dfrac{180^o}{2}=90^o\Rightarrow AH\perp BC\Rightarrow AI\perp BC\) (điều phải chứng minh).
f) Để \(BD=DE=CE\) thì \(\Delta BDE\) cân tại \(D\) và \(\Delta CDE\) cân tại \(E\).
Xét với tam giác BDE, khi đó : \(\hat{DBE}=\hat{DEB}\).
Mà : \(\hat{DEB}=\hat{EBC}\) (do \(DE\left|\right|BC\left(cmt\right)\) và hai góc ở vị trí so le trong).
\(\Rightarrow\hat{DBE}=\hat{EBC}\) ⇒ BE là đường phân giác của \(\hat{B}\).
Tương tự với tam giác CDE thì CD sẽ là đường phân giác của \(\hat{C}\).
Vậy : \(BD=DE=CE\) khi và chỉ khi D, E lần lượt là giao điểm của đường phân giác tại các đỉnh B, C với AC, AB.
Hình vẽ Bài 1.