
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)

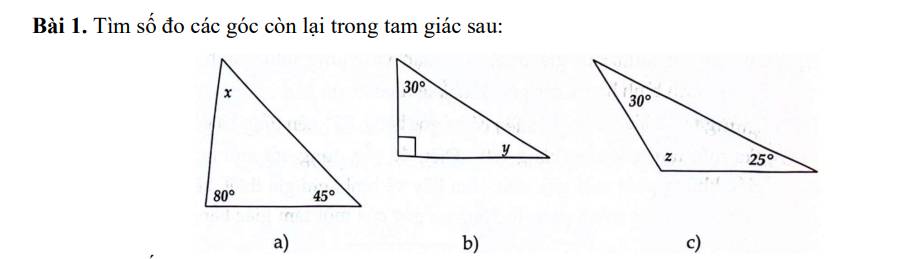
Lời giải:
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$

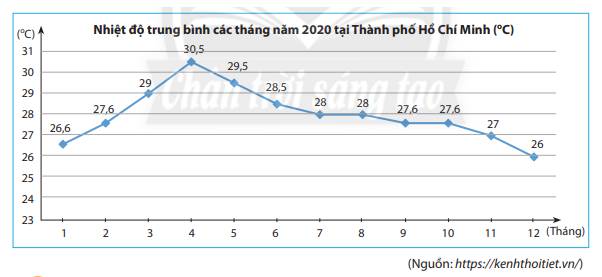
+ Biểu đồ biểu diễn nhiệt độ trung bình các tháng năm 2020 tại Thành phố Hồ Chí Minh.
+ Đơn vị thời gian là tháng, đơn vị số liệu là độ C.
+ Tháng 4 có nhiệt độ trung bình cao nhất.
+ Tháng 12 có nhiệt độ trung bình thấp nhất.
+ Nhiệt độ trung bình tăng trong những khoảng thời gian từ tháng: 1 – 2; 2 – 3; 3 – 4.
+ Nhiệt độ trung bình giảm trong những khoảng thời gian từ tháng: 4 – 5; 5 – 6; 6 – 7; 8 – 9; 10 – 11; 11 – 12.
+ Nhiệt độ trung bình không đổi trong những khoảng thời gian từ tháng: 7 – 8; 9 – 10.

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)

Kẻ Az//Bx//Dy
=> BAD = BAz + DAz = (180o - ABx) + (180o - ADy) = 30o + 60o = 90o





Bài 1. a) Do \(\Delta ABC\) cân tại A (giả thiết) nên \(AB=AC\) và \(\hat{B}=\hat{C}=\dfrac{180^o-\hat{A}}{2}\)
Theo đề bài, \(BD=CE\)
\(\Rightarrow AB-BD=AC-CE\Leftrightarrow AD=AE\).
Suy ra \(\Delta ADE\) cân tại A \(\Rightarrow\hat{D}=\hat{E}=\dfrac{180^o-\hat{A}}{2}\)
Suy ra được : \(\hat{B}=\hat{D}\). Mà hai góc này ở vị trí đồng vị nên \(DE\left|\right|BC\) (điều phải chứng minh).
b) Xét \(\Delta ABE,\Delta ACD\) có : \(\left\{{}\begin{matrix}\hat{A}\text{ chung}\\AD=AE\left(cmt\right)\\AB=AC\left(gt\right)\end{matrix}\right.\Rightarrow\Delta ABE=\Delta ADE\left(c.g.c\right)\)
c) Do \(\Delta ABE=\Delta ACD\left(cmt\right)\) nên \(\hat{DBI}=\hat{ECI}\) (hai góc tương ứng)
Xét các tam giác BID, CIE có : \(\left\{{}\begin{matrix}\hat{DBI}+\hat{DIB}+\hat{BDI}=180^o\\\hat{ECI}+\hat{EIC}+\hat{CIE}=180^o\\\hat{DIB}=\hat{EIC}\left(\text{đối đỉnh}\right);\hat{DBI}=\hat{ECI}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\hat{BDI}=\hat{CIE}\).
Lại xét \(\Delta BID,\Delta CIE\) có : \(\left\{{}\begin{matrix}\hat{BDI}=\hat{CIE}\left(cmt\right)\\BD=CE\left(gt\right)\\\hat{DBI}=\hat{ECI}\left(cmt\right)\end{matrix}\right.\Rightarrow\Delta BID=\Delta CIE\left(g.c.g\right)\) (điều phải chứng minh).
d) Do \(\Delta BID=\Delta CIE\left(cmt\right)\Rightarrow IB=IC\) (hai cạnh tương ứng).
Xét \(\Delta AIB,\Delta AIC\) có : \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\hat{ABI}=\hat{ACI}\left(cmt\right)\\IB=IC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AIB=\Delta AIC\left(c.g.c\right)\Rightarrow\hat{AIB}=\hat{AIC}\)
⇒ \(AI\) là phân giác của \(\hat{BAC}\) (điều phải chứng minh).
e) Gọi \(H\) là giao điểm của \(AI\) và \(BC\).
Xét \(\Delta AHB,\Delta AHC:\) \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\hat{IAB}=\hat{IAC}\left(cmt\right)\\AH\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.g.c\right)\Rightarrow\hat{AHB}=\hat{AHC}\).
Mà : \(\hat{AHB}+\hat{AHC}=180^o\) (hai góc kề bù)
\(\Rightarrow\hat{AHB}=\hat{AHC}=\dfrac{180^o}{2}=90^o\Rightarrow AH\perp BC\Rightarrow AI\perp BC\) (điều phải chứng minh).
f) Để \(BD=DE=CE\) thì \(\Delta BDE\) cân tại \(D\) và \(\Delta CDE\) cân tại \(E\).
Xét với tam giác BDE, khi đó : \(\hat{DBE}=\hat{DEB}\).
Mà : \(\hat{DEB}=\hat{EBC}\) (do \(DE\left|\right|BC\left(cmt\right)\) và hai góc ở vị trí so le trong).
\(\Rightarrow\hat{DBE}=\hat{EBC}\) ⇒ BE là đường phân giác của \(\hat{B}\).
Tương tự với tam giác CDE thì CD sẽ là đường phân giác của \(\hat{C}\).
Vậy : \(BD=DE=CE\) khi và chỉ khi D, E lần lượt là giao điểm của đường phân giác tại các đỉnh B, C với AC, AB.
Hình vẽ Bài 1.