Cho tam giác ABC vuông tại A,đường pg BK (K E AC).Kẻ KI vuông góc với BC,I E BCa c/m tam giác ABK= tam giác IBKb,Kẻ đường cao AH của tam giác ABC.Chứng minh AI là tia pg của góc HACc,gọi F là giao điểm cảu AH và BK.Chứng minh tam giác AFK cân và AF<ACd,lấy điểm m thuộc tia AHsao cho AM=AC.Chứng minh IM vuông góc với IFMọi ng nhớ giúp em với ạ đúng em like ạ .Xin cảm ơn làm câu b,c,d ạ câu a em làm đc rồiAi làm...
Đọc tiếp
Cho tam giác ABC vuông tại A,đường pg BK (K E AC).Kẻ KI vuông góc với BC,I E BC
a c/m tam giác ABK= tam giác IBK
b,Kẻ đường cao AH của tam giác ABC.Chứng minh AI là tia pg của góc HAC
c,gọi F là giao điểm cảu AH và BK.Chứng minh tam giác AFK cân và AF<AC
d,lấy điểm m thuộc tia AHsao cho AM=AC.Chứng minh IM vuông góc với IF
Mọi ng nhớ giúp em với ạ đúng em like ạ .Xin cảm ơn làm câu b,c,d ạ câu a em làm đc rồi
Ai làm nhanh và đúng nhất cho 4 like ạ
~Cảm ơn ~
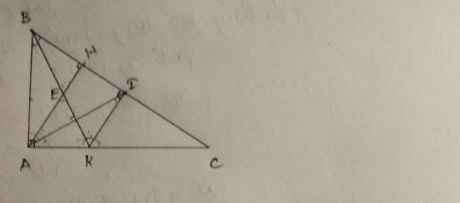
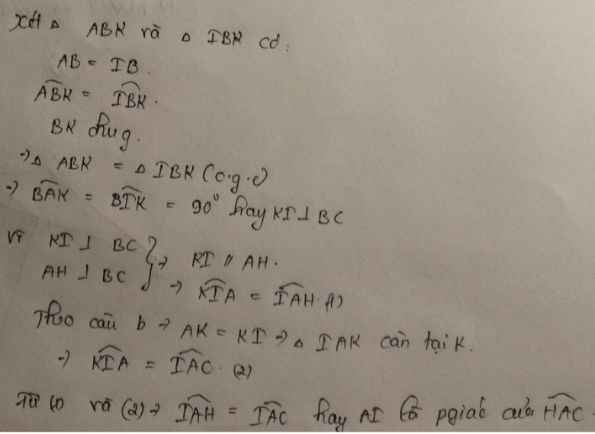
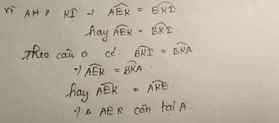
a) Câu này bạn làm được rồi nhưng mình vẫn nói qua:
Tam giác ABK=Tam giác IBK (Cạnh huyền góc nhọn)
b) Từ điểm I vẽ đường thẳng vuông góc với AC, cắt AC tại điểm N.
Ta có: IN vuông góc với AC, AB vuông góc với AC tại A
=> IN//AB (Quan hệ song song vuông góc)
=>^BAI=^NIA (So le trong) (1)
Lại có: Tam giác ABK= Tam giác IBK (Bạn đă c/m đc)=> AB=IB (2 cạnh tương ứng)
=> Tam giác ABI cân tại đỉnh B=> ^BAI=^BIA (hay ^BAI=^HIA) (2 góc ở đáy) (2)
Từ (1) và (2)=> ^HIA=^NIA.
Xét tam giác HAI và tam giác NAI:
^AHI=^ANI=90o
AI chung => Tam giác HAI=Tam giác NAI (Cạnh huyền góc nhọn)
^HIA=^NIA
=> ^HAI=^NAI (2 góc tương ứng)=> AI là phân giác của ^HAN hay AI là phân giác của ^HAC (đpcm)
c)+) AH vuông góc với BC, F thuộc AH; IK cũng vuông góc với BC=> AF song song với IK (Quan hệ song song vuông góc)
=> ^AFK=^IKF (So le trong) (3)
Ta có: Tam giác ABK = Tam giác IBK (Đã cm ở câu a) (Câu a rất quan trọng)
=> ^AKB=^IKB. Mà F cũng thuộc BK=> ^AKF=^IKF (4)
Từ (3) và (4)=> ^AFK=^AKF=> Tam giác AFK cân tại A theo tính chất 2 góc ở đáy của tam giác cân (đpcm)
+) Ta có: AH vuông góc với BC, BC là đường xiên => AH<AC (Quan hệ đường xiên hình chiếu) (5)
Mà F thuộc AH=> AF<AH (6)
Từ (5) và (6)=> AF<AC (đpcm)
d) AM=AC=> AF+FM=AK+KC (7)
Mà tam giác AFK cân tại A=> AF=AK (8)
Từ (7) và (8)=> FM=KC.
AI là phân giác của ^HAC=> AI cũng là phân giác của ^MẠC=> ^MAI=^CAI
Xét tam giác AIM và tam giác AIC:
AI chung
^MAI=^CAI => Tam giác AIM= Tam giác AIC (c.g.c)
AM=AC
=> IM=IC (2 cạnh tương ứng) và ^AMI=^ACI (2 góc tương ứng) (hay ^FMI=^KCI)
Xét tam giác FIM và tam giác KIC:
FM=KC
^FMI=^KCI => Tam giác FIM= Tam giác KIC (c.g.c)
IM=IC
=> ^FIM=^KIC (2 góc tương ứng). Mà KI vuông góc với BC => ^KIC=90o
=> ^FIM=90o => IM vuông góc với IF (đpcm).
khó quá